Core AI For Any Rummy Variant

Step by Step guide to a Rummy AI

Motivation

As I was in the process of developing a reinforcement learning (RL) model for a Rummy game, I reached the stage where I needed an AI opponent to carry out the environment setup and contribute to the model training. However, after searching online, I found that resources for creating an AI for Rummy game were limited, and the few solutions available were too slow for my needs. Since the AI would be used in training, (training time was already high without it) therefore, the AI needed to operate quickly and efficiently in both processing speed and memory use. Needless to say Brute-force solution simply wouldn’t cut it, so I had to experiment with various algorithms and optimization techniques to achieve the complexity and speed appropriate for training.

So Why Read These Article ?

What we’re going to build here is general, adaptable and suitable for almost any type of Rummy game you may be developing. You’ll only need to add your own strategy layer on top of it, then allow the AI to make decisions based on the output of this system. Additionally, you can directly integrate it into your Rummy game to be a tool to help players organize their cards by automatically Dividing them into possible meld combinations. Furthermore, the techniques we’ll implement here can be applied to other areas, so no matter what, I guarantee it will benefit you in one way or another.

Putting Things in Perspective,

This article won’t cover the complete AI; rather, it presents the essential building blocks and core component of the AI, which we’ll refer to as “hand evaluator” system. This hand evaluator analyzes a given Rummy hand and extracts all possible “Combos” that can be formed. It serves as the initial step and forms the groundwork for the AI’s decision-making process, that will be explored in a separate Medium article in the future.

Project Scope and Expectation

Before starting, it’s essential to define the scope of the hand evaluator system we aim to develop. In short, what we are gone build will take a set of n Rummy cards (15 in our case) and output a list of valid combinations, or “combo” that can be extracted from the hand. To keep the system widely adaptable for Rummy variants, we’ll exclude two specific options: first, the use of Joker cards, and second, the option to place the Ace card after the King in a run meld. By setting these rules, the system becomes easier to understand. However, these design choices don’t restrict the system’s adaptability, as it can easily be expanded to include those rules if needed.

Since this hand evaluator will be called repeatedly throughout the gameplay, it must remain optimized and memory efficient.

Moreover, given the nature of Rummy, for the AI to process all potential actions, it needs to evaluate different scenarios by adding or removing cards. To address this, the hand evaluator system must support dynamic hand modifications. Ideally, we want to avoid reprocessing the hand from scratch; instead, we need to use the already processed hand from previous runs of the system to minimize the work required to re-extract combos whenever the hand is modified.

Key Terminology and Setup

Deck: the deck will contain 104 card with 52 Unique card and each card is duplicated once with a total of 13 * 4 * 2 = 104.

Card Ranks: from 1 to 13  with ranks 11, 12, and 13 representing the Jack, Queen, and King, respectively.

Card Suits: The four suits are Hearts, Spades, Clubs, and Diamonds, which can also be indicated by H, S, C, and D, or with icon respectively.

Run: A sequence of three or more consecutive cards of the same suit.
Example: 3H | 4H | 5H

Set: A group of three or four cards with the same rank but different suits.
Example: 6H | 6S | 6D

Dump: A group of cards that couldn’t be used to create or be added to valid melds.

Combo: One possible division of a hand into runs, sets, and dump.

Example:

Hand:
3H | 4H | 5H | 6H | 7H | 7C | 7S | 6S | 10S | JD | 6D | KH | 2C | 3D | 4S

One Possible Combo:

· Run: 3H | 4H | 5H | 6H

· Set: 7H | 7C | 7S

· Dump: 6S | 10S | JD | 6D | KH | 2C | 3D | 4S

System Breakdown

Identifying and Collecting key Data

I explored several algorithms to optimize and reduce the search space for all possible combos. However, the fact that each card can appear twice increased the number of potential combos, making it challenging to track and validate each one. While competing on Codeforces, I encountered a problem that reminded me of the ‘island problem,’ which gave me new insight into approaching the hand evaluator system.

We can represent the hand as a 2D grid of size 4x13, where each column represents ranks from 1 to 13 and each row corresponds to the 4 suits. Each cell in this grid contains the count of cards in the hand in our case either 1, 2, or 0 . This allows us to divide the hand into ‘islands,’ which are defined as groups of connected land cells with counts of 1 or 2 based on the following connectivity rules:

1. Two cells are considered connected if they share a side (left, right, above, or below) in the grid.

2. All cells within the same column are also connected if they both contain at least 1s, even if they are not adjacent (above or below).

EXP of ‘ hand A’ : 11C 3H 4H 11D 3D 5H 9D 2H 6H 3C 4H 3D 4D 5H 12D 3C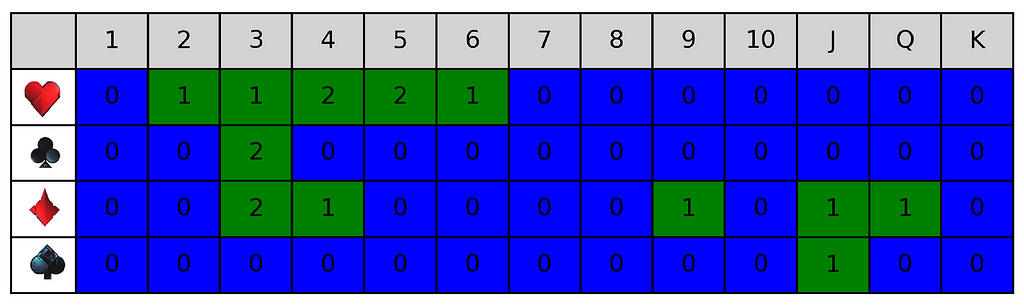

Our first task is to identify and label all distinct islands. Since each island is independent of the others, we can make our life easier by mapping each island to a class type let’s name it _cardGraph. This class will be responsible for that island in terms of extracting, modifying, or deleting operations.

For clarity, let’s isolate one island and work on it in the upcoming sections, so it’s easier for you to follow. If it helps, you can think of each island as a connected graph, as Shown in the figure below: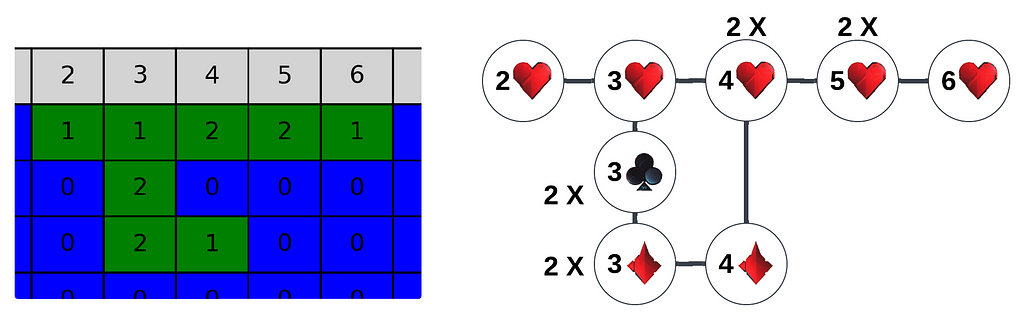

Now If you take multiple island examples and try to extract the possible combos, you’ll notice that some cards have unique roles in branching out to a potential combinations. We’ll call these type of cards a control points or Cpts for short, as they play an essential role by reducing the search space significantly as you will see in the following steps.

Cpts: For a card to be considered a Cpts, it must be in a position where we have to make a choice on which meld (run or set) to append it to. If a card can naturally fit into multiple melds without forcing a choice (for example, a duplicate card with two options for melds each card will append to a meld), it won’t be considered a Cpts.

In the case of our island example the 3 of heart is identified as a cpts. Below are all the melds that the 3 of Hearts could attach to, one at a time.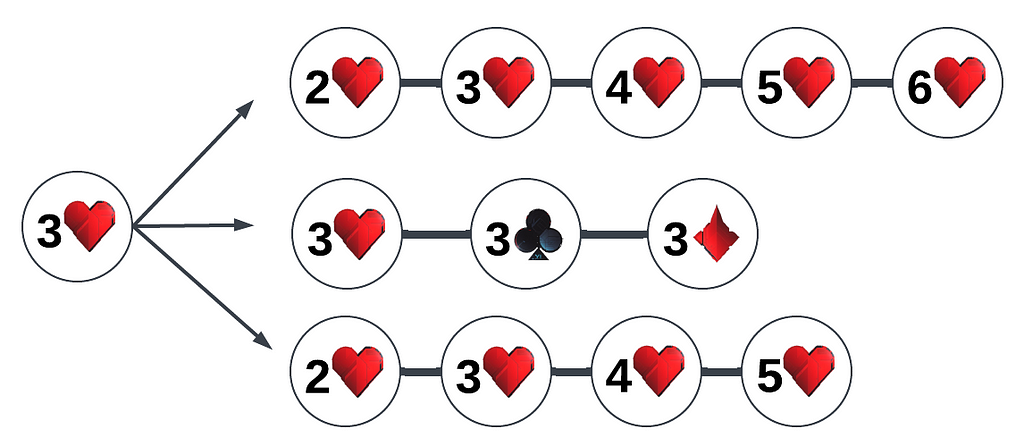

Our next step is to mark each card that qualifies as a Cpts. To do this, we’ll create a 4x13 (in byte type) table lets call it _flagMap . Now for memory efficiency, you can make this a shared table each _cardGraph instance created from the hand can reference it and use it . In this table, each card in an island will be assigned a bitstream at the corresponding index in _flagMap, this byte will represents its potential placements in different runs or sets. If a card qualifies as a Cpts, it will be stored in a stack (we will need later), which we’ll call _cptsStack. Here’s a breakdown of the byte structure: the first bit indicates whether the card belongs to a run, the second bit indicates its placement in an additional run, the third bit represents whether it belongs to a set, and the fourth bit specifies if it belongs to multiple sets.

Here’s an example of a bitstream: 00000111 In here we have:

• The first bit (1) means the card can belong to a run.

• The second bit (1) means the card can belong to a second run.

• The third bit (1) means the card belongs to a set.

• The fourth bit (0) means the card doesn’t belong to a second set.

We might be in case where the configuration is 00000101 for one card (no copy), meaning the card belongs to a run or a set. Or another configuration could be 00000011, meaning the card belongs to two different runs.

To identify a cpts, simply count the ‘1’s in its bit representation. If this count exceeds the total number of that card in the hand, it’s considered a cpts. For instance, if a card appears twice (i.e., has two copies) and its bit representation is 00000101, it’s not a cpts. However, if the bit representation is 00000111 like the example , then it qualifies as a cpts.

In our island example, here’s how the _flagMap table would look :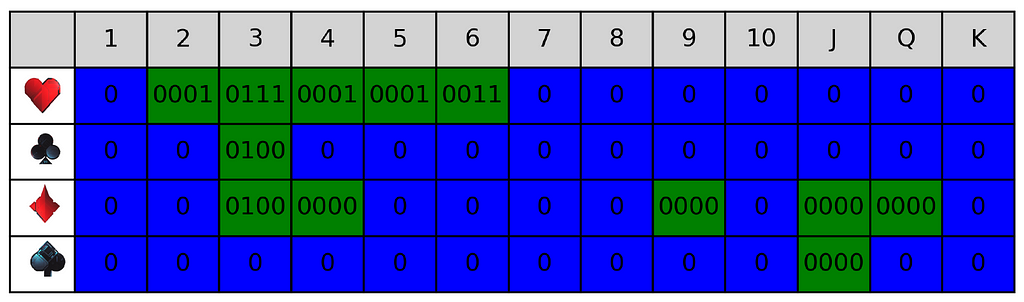

Once we’ve populated the _flagMap and identified the cpts, the next task is to decompose the island into horizontal and vertical lines. But why? Breaking down the card graph into these lines simplifies the process of identifying runs and sets, as it allows us to focus on contiguous sequences of cards that can be processed more efficiently. As you might guess, the vertical lines will represent the sets, while the horizontal lines will represent the runs.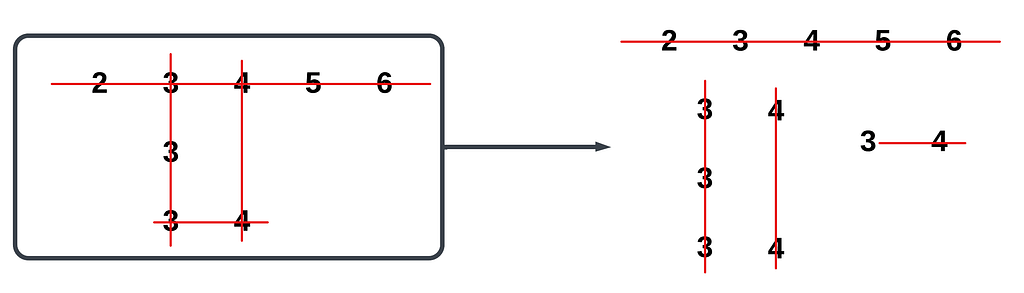

We’ll store each horizontal line in a list of a tuple type, where the first item represents the starting index of the line and the last item represents the end index (inclusive). For the vertical lines, it’s sufficient to simply store the column index in a list.

Tip: We can accomplish this task along with the bit representation step in a single loop, achieving O(n) complexity.

Generate Combos

Now, let’s take a break and recap: we have identified the control points (CPTs) and stored them in the _cptsStack. We also decomposed the island into vertical and horizontal lines, and populated the _flagMap with card bit representation.

With our data in place, what remains is to use it to generate all possible valid combos of the island. But how do we do that? Here’s a simplified approach:

1. Assign Valid Placements for the Control Points (Cpts):
We take the bit representation of a cpts from _flagMap, which indicates all possible placements for that cpts. Then, we look at the number of copies of the cpts in the _cardGraph and adjust its bit representation to a current valid configuration. For example, if the cpts has a bit representation of 00001111 and 2 copies, we can generate all valid placements for it, which is C(4,2)=6C(4,2) = 6C(4,2)=6. Possible combinations would be 0011, 0101, 1100, 1010, 1001, and 0110.

2. Using DFS to Configure All Possible Combinations for Each Cpts:
We’ll use a depth-first search (DFS) to iterate over the valid placements for each cpts as shown in step 1. Each node in the DFS tree represents a possible placement for a given cpts, so each unique DFS path represents a valid combo configuration. For each “leaf” node (end of the DFS path), we proceed to the next step.

3. Generating Combos:
In this step, we iterate over the horizontal and vertical lines in the island to identify runs, sets, and a dump list. This is done in two passes for each line, as follows:

• Pass 1: For a horizontal line, for example, we continuously append cards from [line start to line end] into a list to form a run. We stop adding if ( card_bit_representation | 00000001 == 0 ). If the length of the run is greater than or equal to 3, we add it to the run combo; otherwise, each card goes into the dump list, and we continue trying to form another run until we reach the line end.
• Pass 2: Repeat the process, this time looking for cards that match a different bit pattern with or operation ( 00000010). This allows us to identify possible second runs.

The same approach applies to extracting sets, but we use bit operations with 00000100 and 00001000.

4. Register the Valid Combo and Move to the Next DFS Configuration:
After completing all runs, sets, and dumps for the current combo, we save the combo and then move on to the next DFS configuration to repeat the process. This way, we systematically explore all potential configurations for valid combos.

Demo Output

if you coded everything correctly and feed it our island example : ”2H3H4H5H4H5H6H3C3C3D3D4D”, it should be decomposed as shown bellow. Notice that I’ve added some calculation to each generated combo so that we can get a sense of how the AI will act.

What’s Next?

In the next article, I’ll dive into the rest of the system, focusing on the dynamic modification of the hand and the AI strategy. If you’ve followed along so far, it won’t be hard to see how we can optimize adding and removing cards, as well as incorporate the two rules we set aside at the beginning. Stay tuned, and see you next time! “hopefully ????”.

Unless otherwise noted, all images are created by the author using Lucidchart ,Gimp and Python

Core AI For Any Rummy Variant was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.