Lasso and Elastic Net Regressions, Explained: A Visual Guide with Code Examples

REGRESSION ALGORITHM

Roping in key features with coordinate descent

Least Squares Regression, Explained: A Visual Guide with Code Examples for Beginners

Linear regression comes in different types: Least Squares methods form the foundation, from the classic Ordinary Least Squares (OLS) to Ridge regression with its regularization to prevent overfitting. Then there’s Lasso regression, which takes a unique approach by automatically selecting important factors and ignoring others. Elastic Net combines the best of both worlds, mixing Lasso’s feature selection with Ridge’s ability to handle related features.

It’s frustrating to see many articles treat these methods as if they’re basically the same thing with minor tweaks. They make it seem like switching between them is as simple as changing a setting in your code, but each actually uses different approaches to solve their optimization problems!

While OLS and Ridge regression can be solved directly through matrix operations, Lasso and Elastic Net require a different approach — an iterative method called coordinate descent. Here, we’ll explore how this algorithm works through clear visualizations. So, let’s saddle up and lasso our way through the details!

Definition

Lasso Regression

LASSO (Least Absolute Shrinkage and Selection Operator) is a variation of Linear Regression that adds a penalty to the model. It uses a linear equation to predict numbers, just like Linear Regression. However, Lasso also has a way to reduce the importance of certain factors to zero, which makes it useful for two main tasks: making predictions and identifying the most important features.

Elastic Net Regression

Elastic Net Regression is a mix of Ridge and Lasso Regression that combines their penalty terms. The name “Elastic Net” comes from physics: just like an elastic net can stretch and still keep its shape, this method adapts to data while maintaining structure.

The model balances three goals: minimizing prediction errors, keeping the size of coefficients small (like Lasso), and preventing any coefficient from becoming too large (like Ridge). To use the model, you input your data’s feature values into the linear equation, just like in standard Linear Regression.

The main advantage of Elastic Net is that when features are related, it tends to keep or remove them as a group instead of randomly picking one feature from the group.

???? Dataset Used

To illustrate our concepts, we’ll use our standard dataset that predicts the number of golfers visiting on a given day, using features like weather outlook, temperature, humidity, and wind conditions.

For both Lasso and Elastic Net to work effectively, we need to standardize the numerical features (making their scales comparable) and apply one-hot-encoding to categorical features, as both models’ penalties are sensitive to feature scales.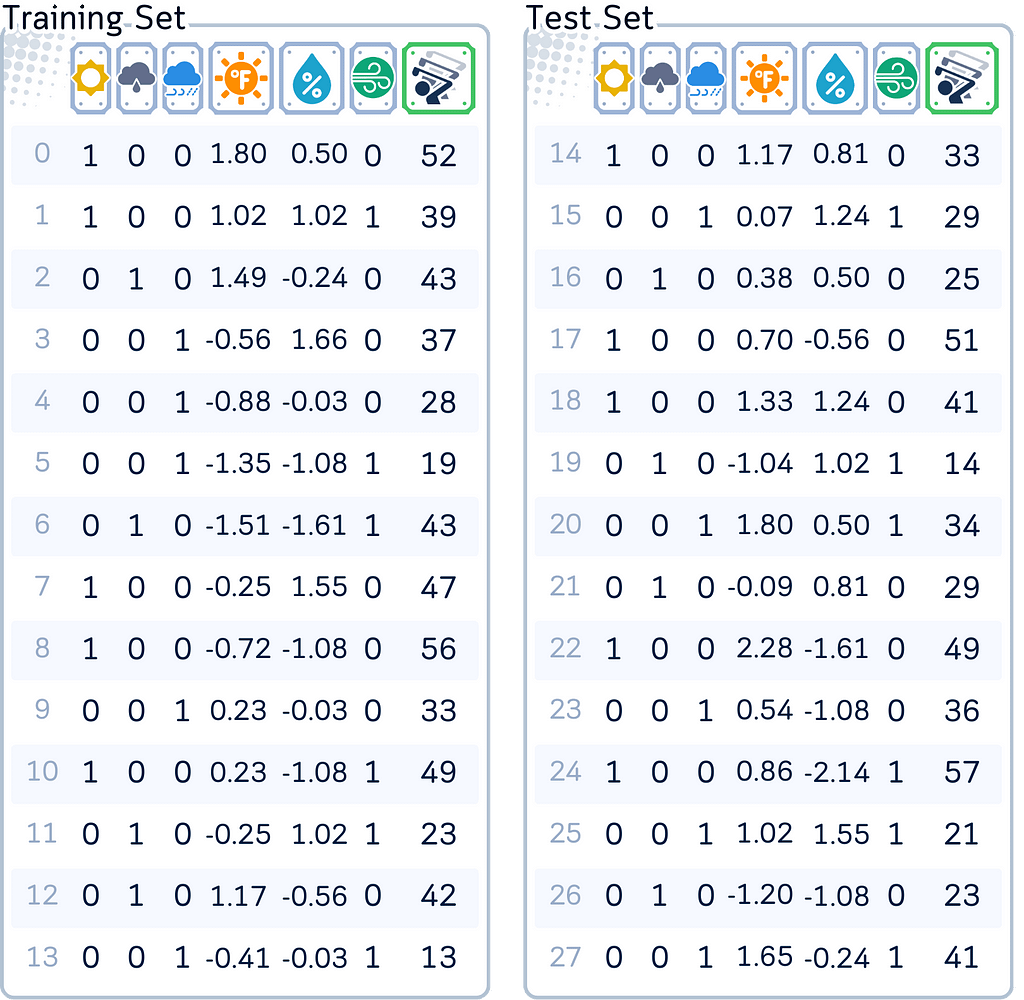

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.compose import ColumnTransformer

# Create dataset
data = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 
                'rain', 'sunny', 'overcast', 'overcast', 'rain', 'sunny', 'overcast', 'rain', 'sunny', 
                'sunny', 'rain', 'overcast', 'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
    'Temperature': [85, 80, 83, 70, 68, 65, 64, 72, 69, 75, 75, 72, 81, 71, 81, 74, 76, 78, 82, 
                   67, 85, 73, 88, 77, 79, 80, 66, 84],
    'Humidity': [85, 90, 78, 96, 80, 70, 65, 95, 70, 80, 70, 90, 75, 80, 88, 92, 85, 75, 92, 
                 90, 85, 88, 65, 70, 60, 95, 70, 78],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, 
             True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
    'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29, 25, 51, 41, 
                    14, 34, 29, 49, 36, 57, 21, 23, 41]
}

# Process data
df = pd.get_dummies(pd.DataFrame(data), columns=['Outlook'])
df['Wind'] = df['Wind'].astype(int)

# Split data
X, y = df.drop(columns='Num_Players'), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)

# Scale numerical features
numerical_cols = ['Temperature', 'Humidity']
ct = ColumnTransformer([('scaler', StandardScaler(), numerical_cols)], remainder='passthrough')

# Transform data
X_train_scaled = pd.DataFrame(
    ct.fit_transform(X_train),
    columns=numerical_cols + [col for col in X_train.columns if col not in numerical_cols],
    index=X_train.index
)

X_test_scaled = pd.DataFrame(
    ct.transform(X_test),
    columns=X_train_scaled.columns,
    index=X_test.index
)

Main Mechanism

Lasso and Elastic Net Regression predict numbers by making a straight line (or hyperplane) from the data, while controlling the size of coefficients in different ways:

1. Both models find the best line by balancing prediction accuracy with coefficient control. They work to make the gaps between real and predicted values small, while keeping coefficients in check through penalty terms.
2. In Lasso, the penalty (controlled by λ) can shrink coefficients to exactly zero, removing features entirely. Elastic Net combines two types of penalties: one that can remove features (like Lasso) and another that shrinks groups of related features together. The mix between these penalties is controlled by the l1_ratio (α).
3. To predict a new answer, both models multiply each input by its coefficient (if not zero) and add them up, plus a starting number (intercept/bias). Elastic Net often keeps more features than Lasso but with smaller coefficients, especially when features are correlated.
4. The strength of penalties affects how the models behave:
   - In Lasso, larger λ means more coefficients become zero
   - In Elastic Net, λ controls overall penalty strength, while α determines the balance between feature removal and coefficient shrinkage
   - When penalties are very small, both models act more like standard Linear Regression

Training Steps

Let’s explore how Lasso and Elastic Net learn from data using the coordinate descent algorithm. While these models have complex mathematical foundations, we’ll focus on understanding coordinate descent — an efficient optimization method that makes the computation more practical and intuitive.

Coordinate Descent for Lasso Regression

The optimization problem of Lasso Regression is as follows: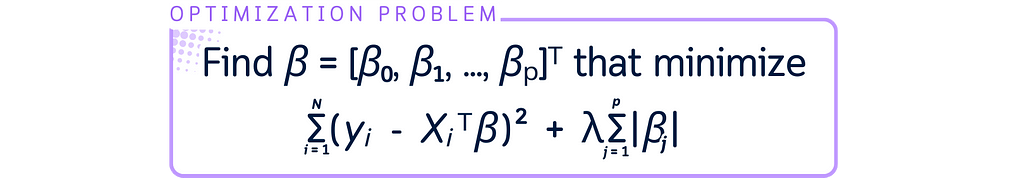

Here’s how coordinate descent finds the optimal coefficients by updating one feature at a time:

1. Start by initializing the model with all coefficients at zero. Set a fixed value for the regularization parameter that will control the strength of the penalty.

2. Calculate the initial bias by taking the mean of all target values.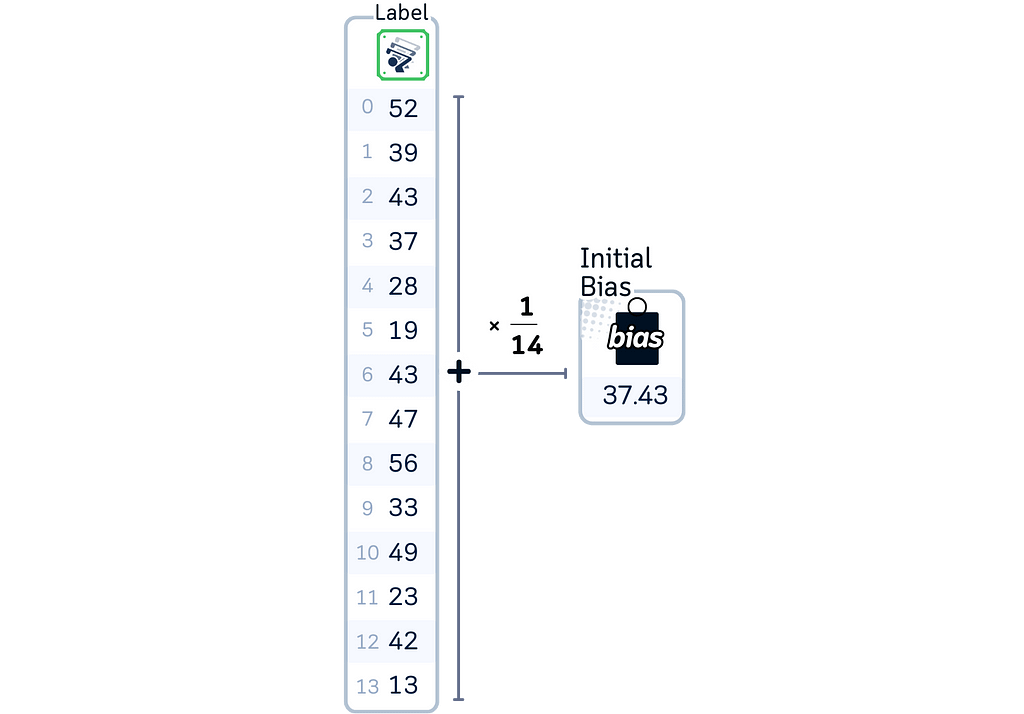

3. For updating the first coefficient (in our case, ‘sunny’):
- Using weighted sum, calculate what the model would predict without using this feature.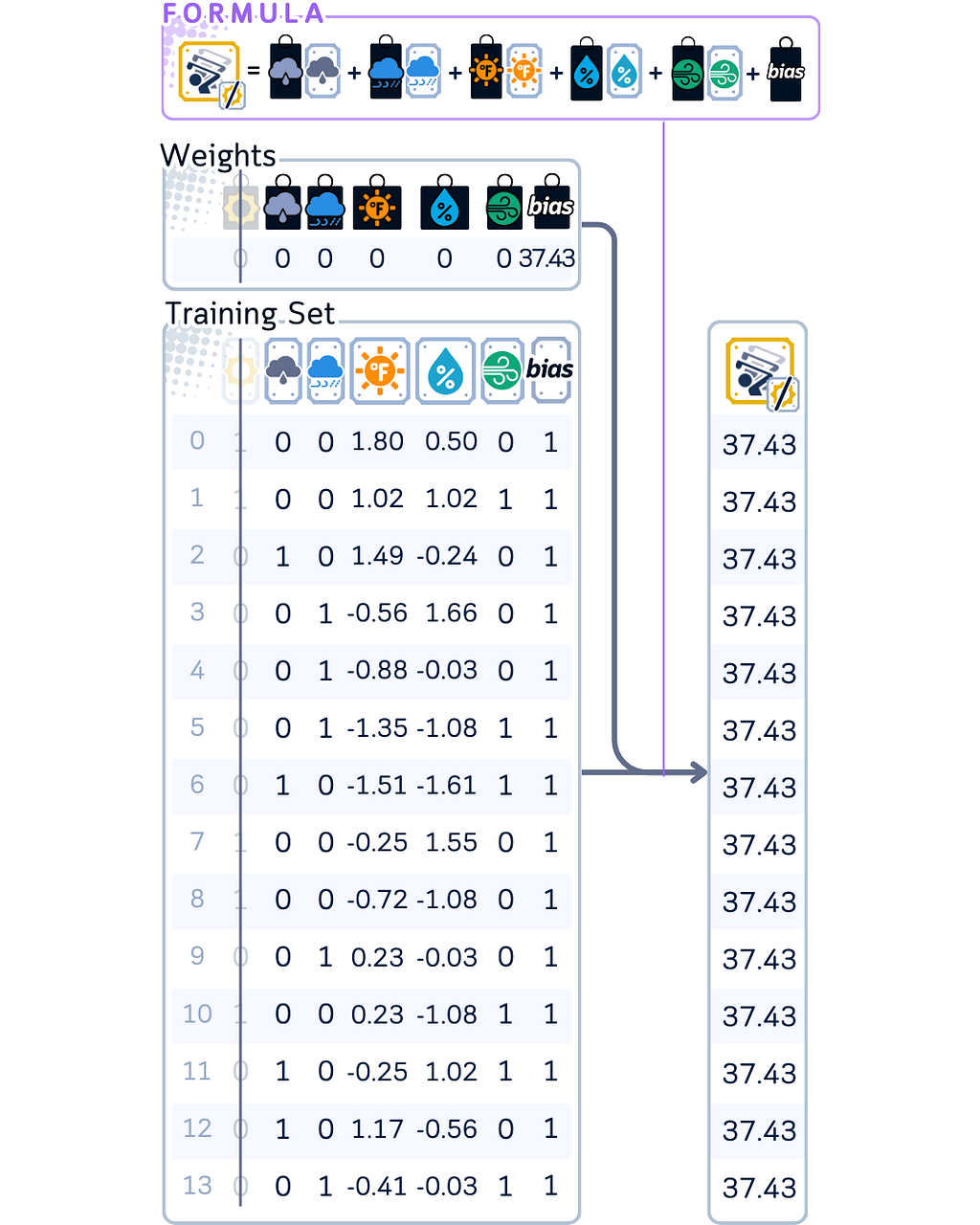

- Find the partial residual — how far off these predictions are from the actual values. Using this value, calculate the temporary coefficient.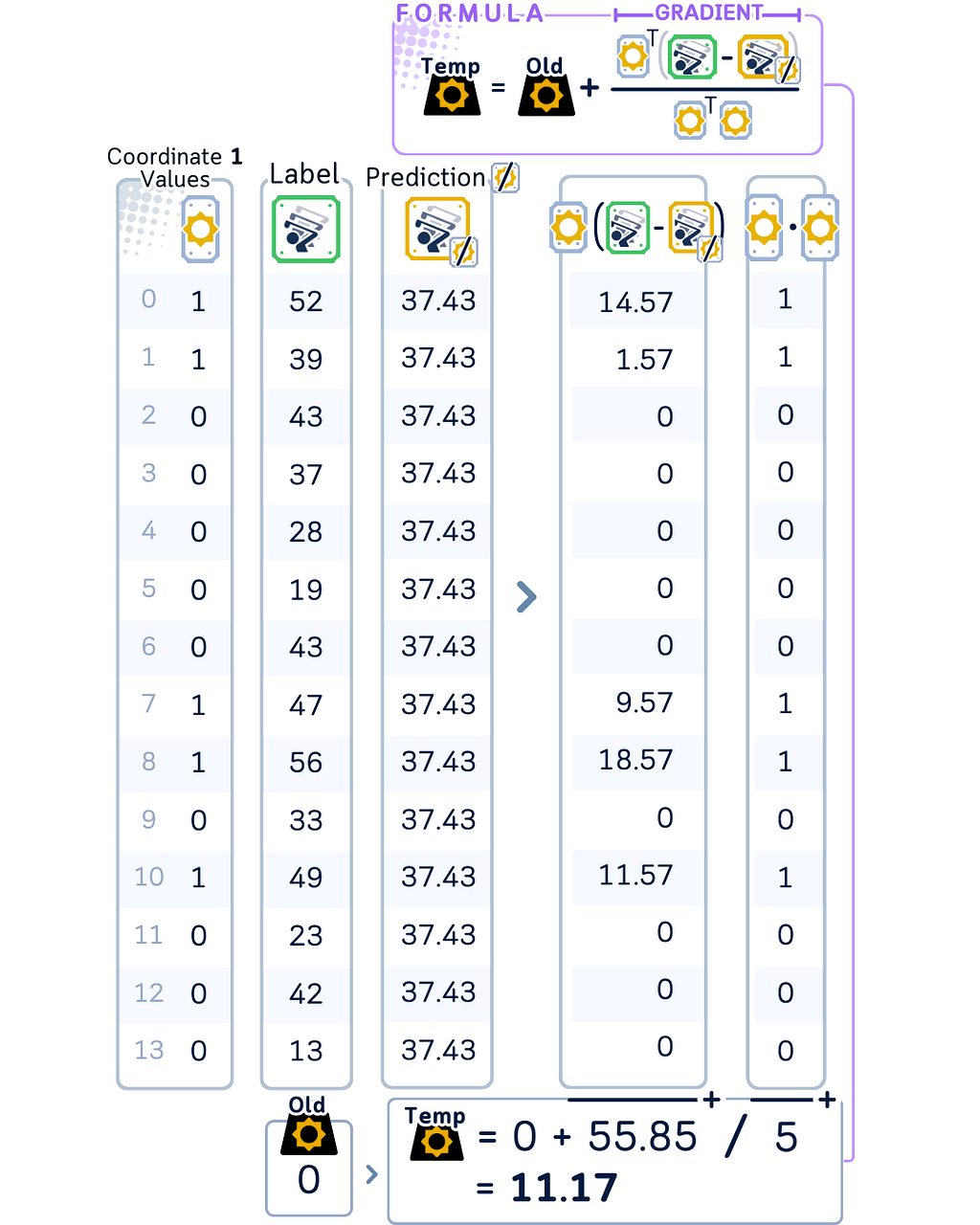

- Apply the Lasso shrinkage (soft thresholding) to this temporary coefficient to get the final coefficient for this step.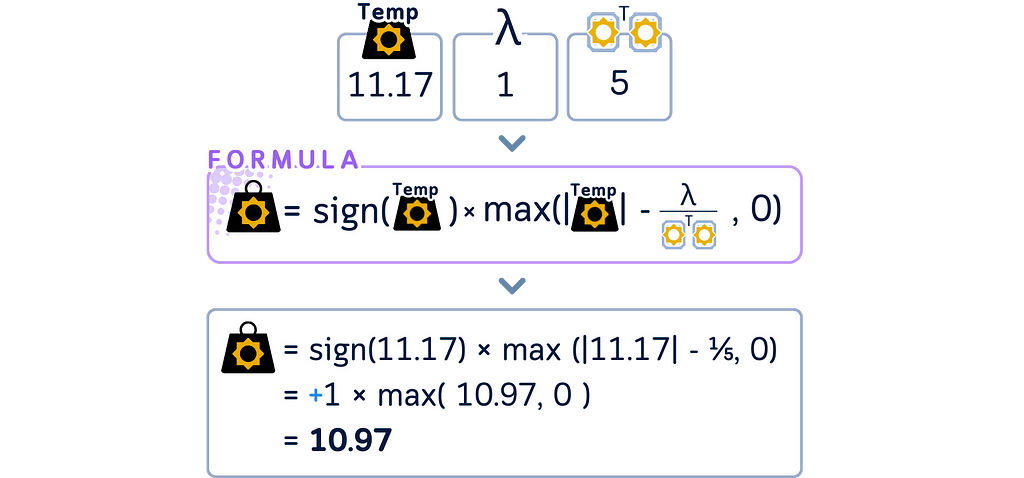

4. Move through each remaining coefficient one at a time, repeating the same update process. When calculating predictions during each update, use the most recently updated values for all other coefficients.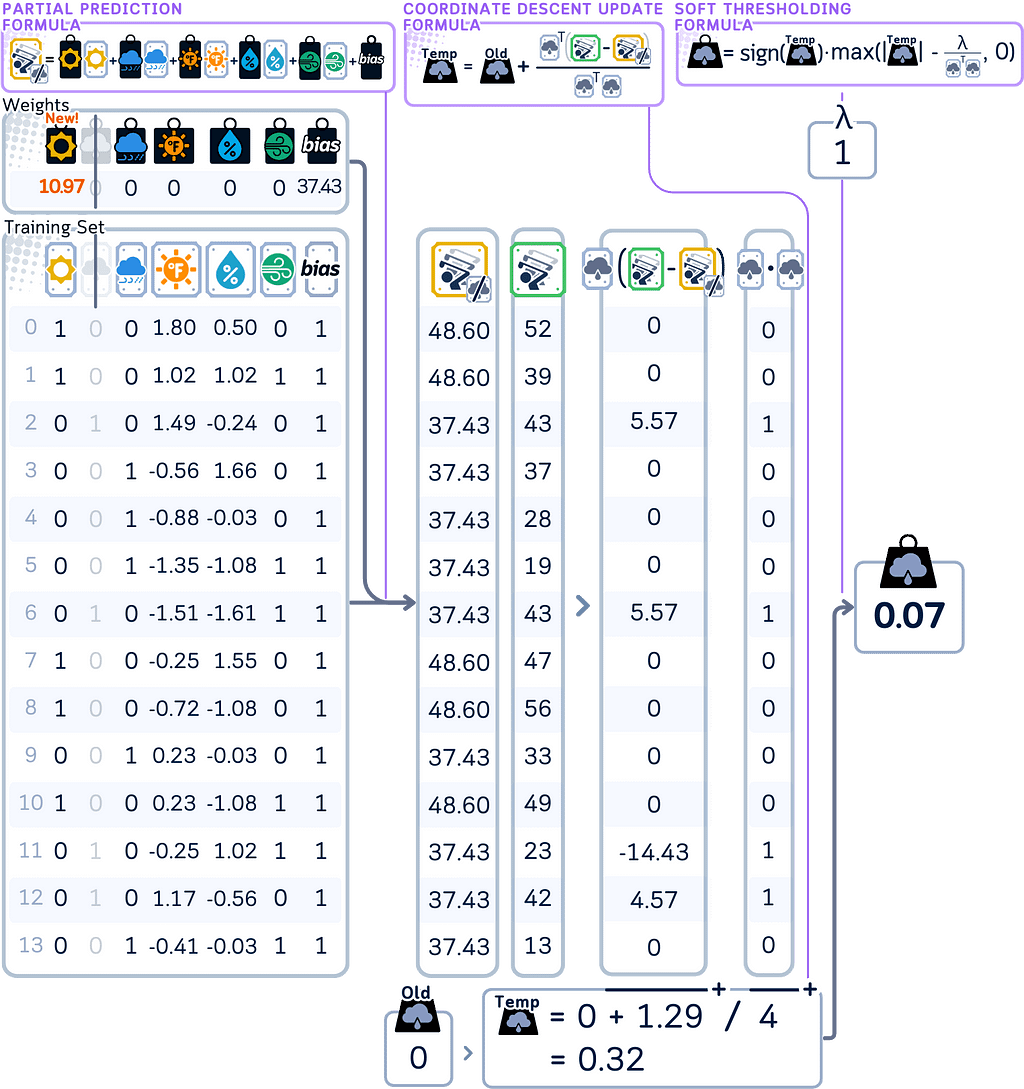

import numpy as np

# Initialize bias as mean of target values and coefficients to 0
bias = np.mean(y_train)
beta = np.zeros(X_train_scaled.shape[1])
lambda_param = 1

# One cycle through all features
for j, feature in enumerate(X_train_scaled.columns):
    # Get current feature values
    x_j = X_train_scaled.iloc[:, j].values

    # Calculate prediction excluding the j-th feature
    y_pred_no_j = bias + X_train_scaled.values @ beta - x_j * beta[j]

    # Calculate partial residuals
    residual_no_j = y_train.values - y_pred_no_j

    # Calculate the dot product of x_j with itself (sum of squared feature values)
    sum_squared_x_j = np.dot(x_j, x_j)

    # Calculate temporary beta without regularization (raw update)
    beta_old = beta[j]
    beta_temp = beta_old + np.dot(x_j, residual_no_j) / sum_squared_x_j

    # Apply soft thresholding for Lasso penalty
    beta[j] = np.sign(beta_temp) * max(abs(beta_temp) - lambda_param / sum_squared_x_j, 0)

# Print results
print("Coefficients after one cycle:")
for feature, coef in zip(X_train_scaled.columns, beta):
    print(f"{feature:11}: {coef:.2f}")

5. Return to update the bias by calculating what the current model predicts using all features, then adjust the bias based on the average difference between these predictions and actual values.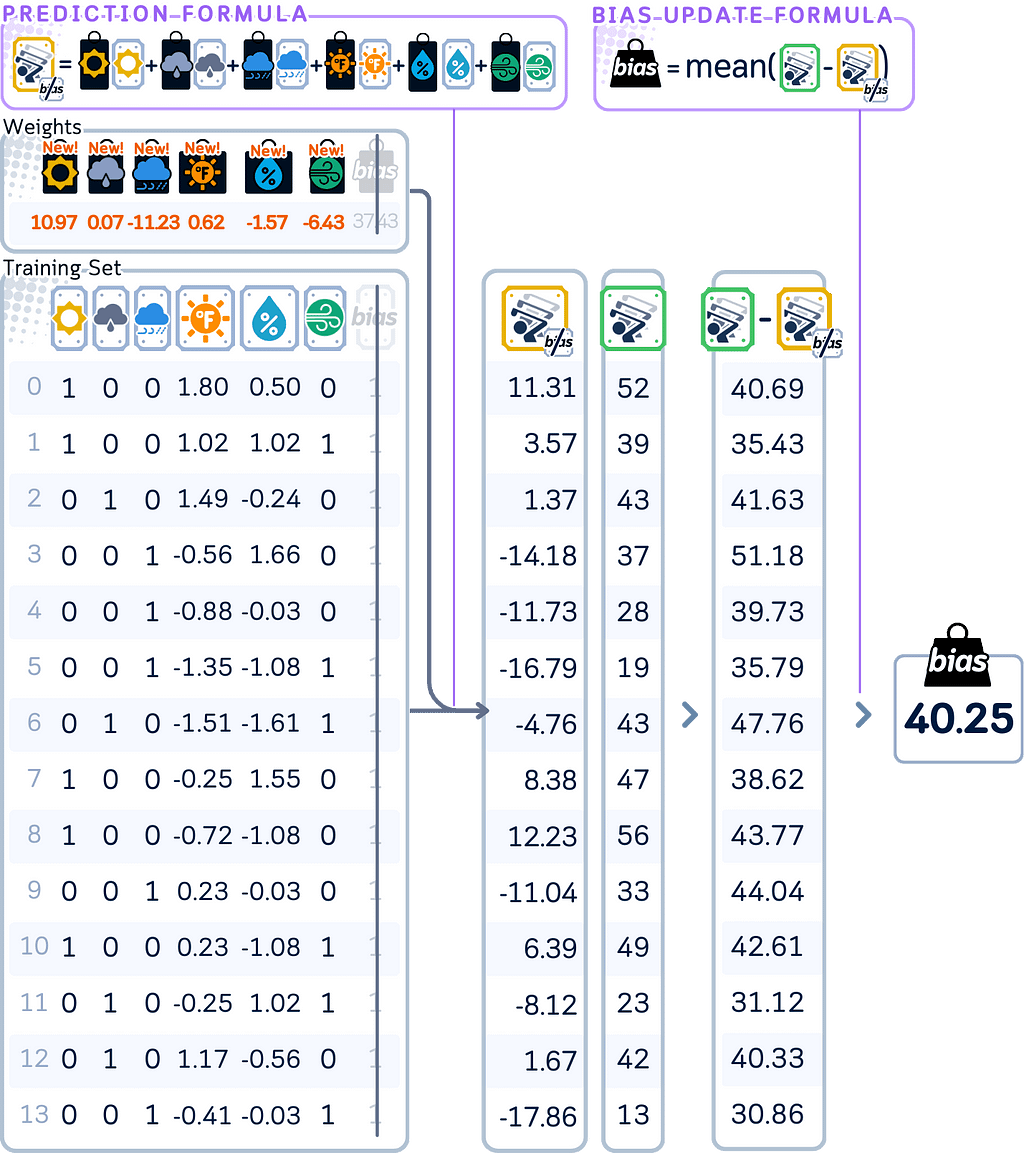

# Update bias (not penalized by lambda)
y_pred = X_train_scaled.values @ beta  # only using coefficients, no bias
residuals = y_train.values - y_pred
bias = np.mean(residuals)  # this replaces the old bias

6. Check if the model has converged either by reaching the maximum number of allowed iterations or by seeing that coefficients aren’t changing much anymore. If not converged, return to step 3 and repeat the process.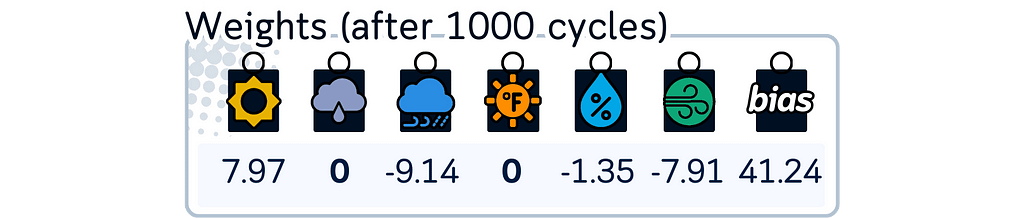

from sklearn.linear_model import Lasso

# Fit Lasso from scikit-learn
lasso = Lasso(alpha=1) # Default value is 1000 cycle
lasso.fit(X_train_scaled, y_train)

# Print results
print("\nCoefficients after 1000 cycles:")
print(f"Bias term  : {lasso.intercept_:.2f}")
for feature, coef in zip(X_train_scaled.columns, lasso.coef_):
   print(f"{feature:11}: {coef:.2f}")

Coordinate Descent for Elastic Net Regression

The optimization problem of Elastic Net Regression is as follows: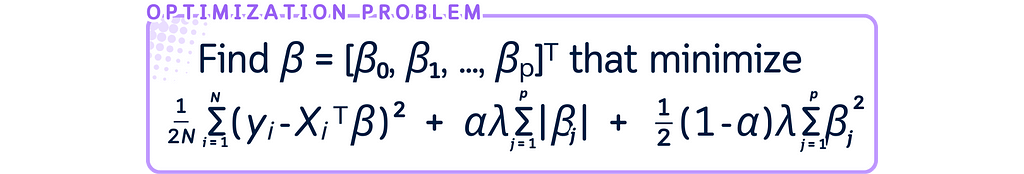

The coordinate descent algorithm for Elastic Net works similarly to Lasso, but accounts for both penalties when updating coefficients. Here’s how it works:

1. Start by initializing the model with all coefficients at zero. Set two fixed values: one controlling feature removal (like in Lasso) and another for general coefficient shrinkage (the key difference from Lasso).

2. Calculate the initial bias by taking the mean of all target values. (Same as Lasso)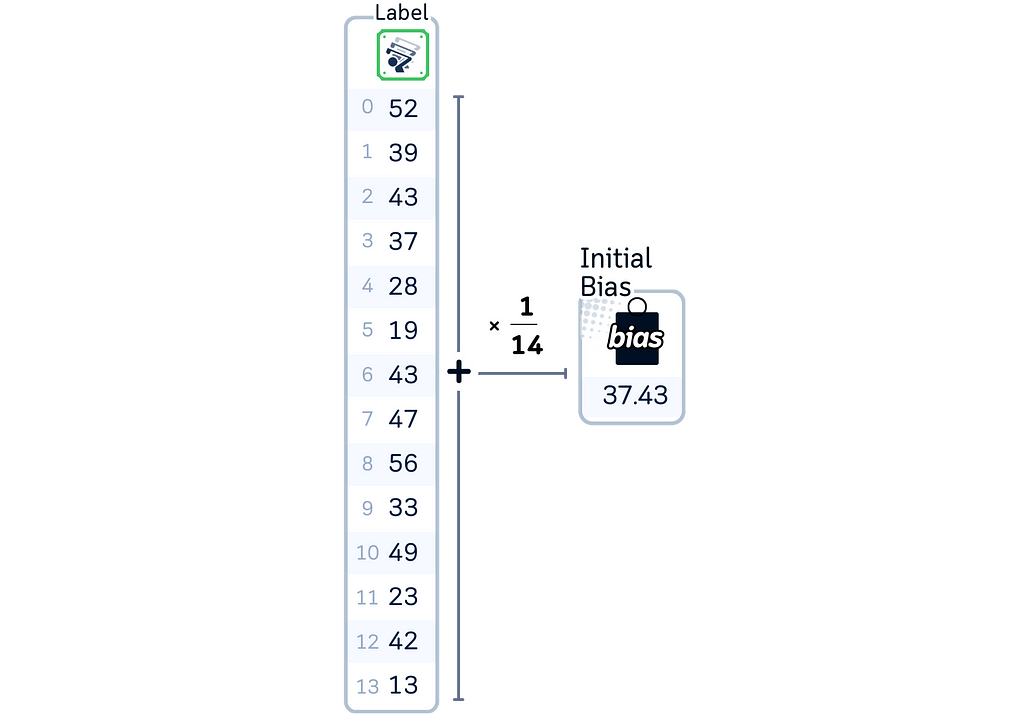

3. For updating the first coefficient:
- Using weighted sum, calculate what the model would predict without using this feature. (Same as Lasso)

- Find the partial residual — how far off these predictions are from the actual values. Using this value, calculate the temporary coefficient. (Same as Lasso)

- For Elastic Net, apply both soft thresholding and coefficient shrinkage to this temporary coefficient to get the final coefficient for this step. This combined effect is the main difference from Lasso Regression.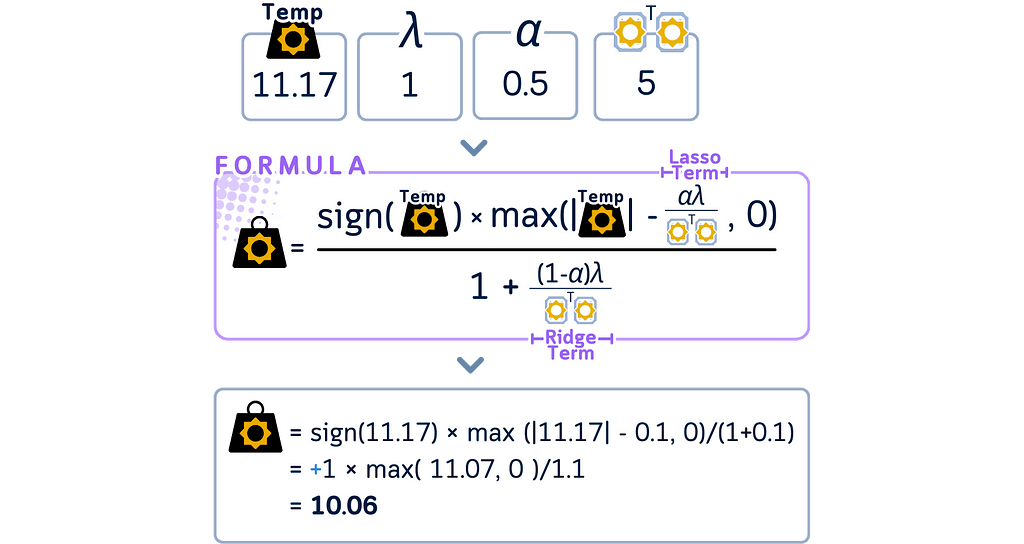

4. Move through each remaining coefficient one at a time, repeating the same update process. When calculating predictions during each update, use the most recently updated values for all other coefficients. (Same process as Lasso, but using the modified update formula)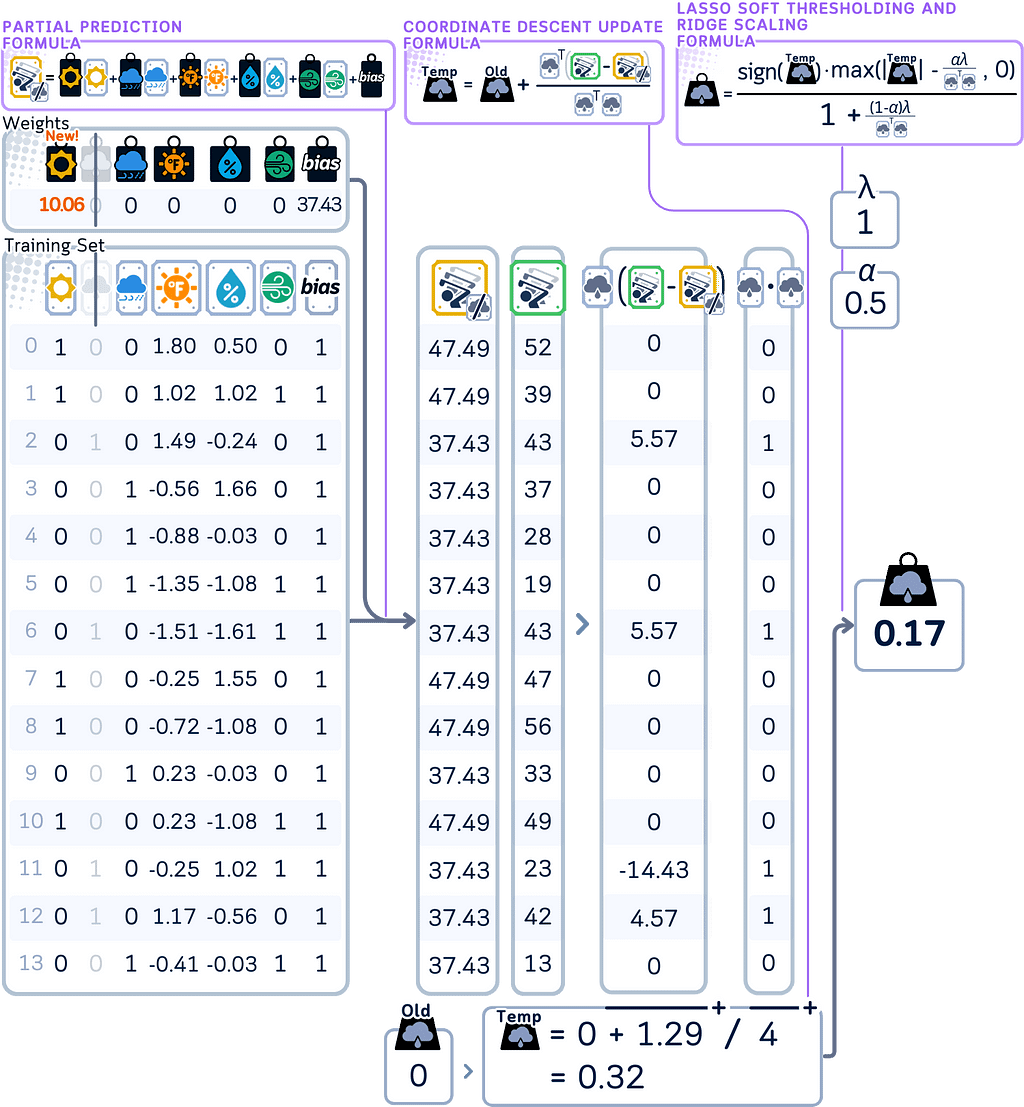

import numpy as np

# Initialize bias as mean of target values and coefficients to 0
bias = np.mean(y_train)
beta = np.zeros(X_train_scaled.shape[1])
lambda_param = 1
alpha = 0.5  # mixing parameter (0 for Ridge, 1 for Lasso)

# One cycle through all features
for j, feature in enumerate(X_train_scaled.columns):
    # Get current feature values
    x_j = X_train_scaled.iloc[:, j].values

    # Calculate prediction excluding the j-th feature
    y_pred_no_j = bias + X_train_scaled.values @ beta - x_j * beta[j]

    # Calculate partial residuals
    residual_no_j = y_train.values - y_pred_no_j

    # Calculate the dot product of x_j with itself (sum of squared feature values)
    sum_squared_x_j = np.dot(x_j, x_j)

    # Calculate temporary beta without regularization (raw update)
    beta_old = beta[j]
    beta_temp = beta_old + np.dot(x_j, residual_no_j) / sum_squared_x_j

    # Apply soft thresholding for Elastic Net penalty
    l1_term = alpha * lambda_param / sum_squared_x_j     # L1 (Lasso) penalty term
    l2_term = (1-alpha) * lambda_param / sum_squared_x_j # L2 (Ridge) penalty term
    
    # First apply L1 soft thresholding, then L2 scaling
    beta[j] = (np.sign(beta_temp) * max(abs(beta_temp) - l1_term, 0)) / (1 + l2_term)

# Print results
print("Coefficients after one cycle:")
for feature, coef in zip(X_train_scaled.columns, beta):
    print(f"{feature:11}: {coef:.2f}")

5. Update the bias by calculating what the current model predicts using all features, then adjust the bias based on the average difference between these predictions and actual values. (Same as Lasso)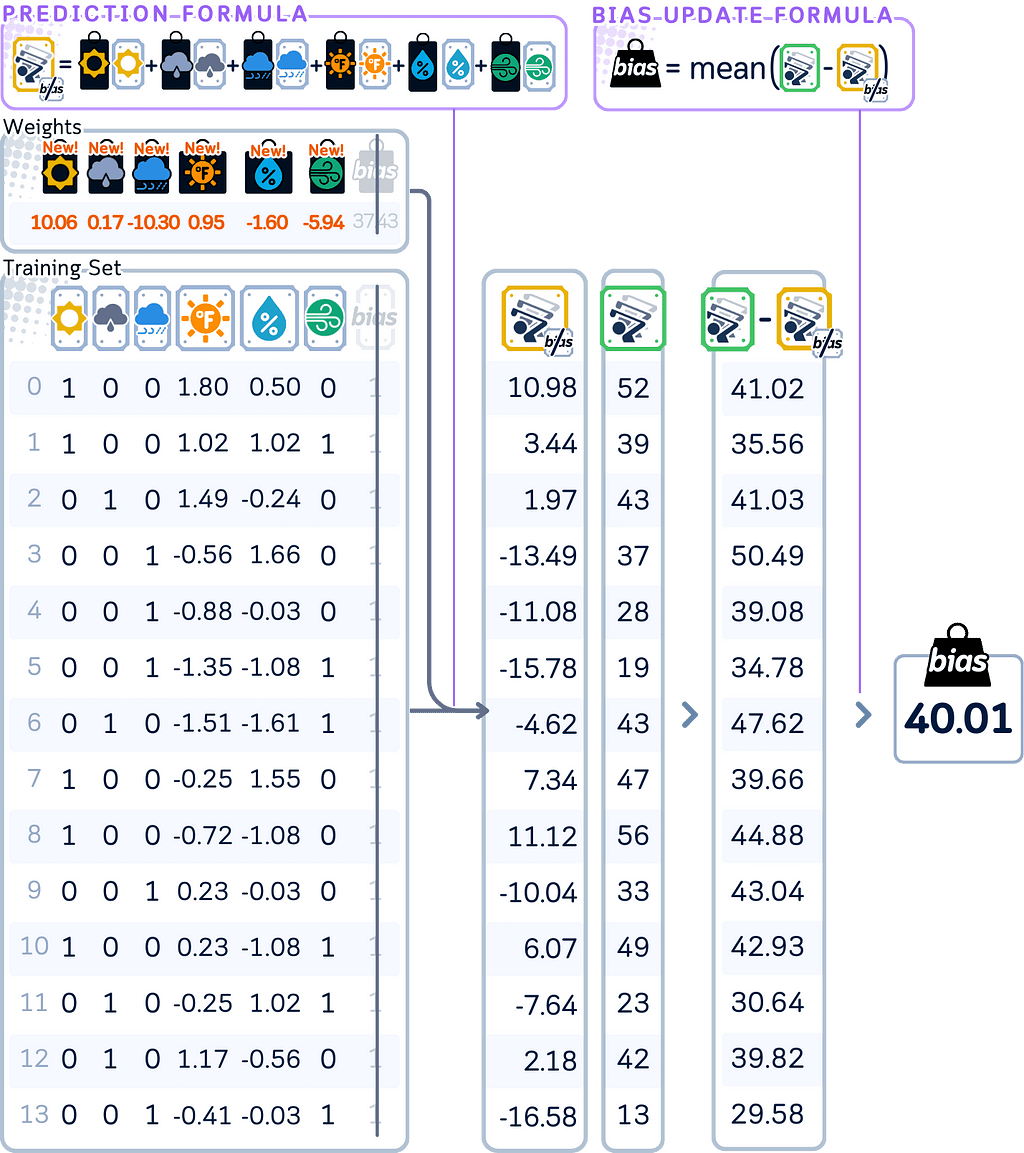

# Update bias (not penalized by lambda)
y_pred_with_updated_beta = X_train_scaled.values @ beta  # only using coefficients, no bias
residuals_for_bias_update = y_train.values - y_pred_with_updated_beta
new_bias = np.mean(y_train.values - y_pred_with_updated_beta)  # this replaces the old bias

print(f"Bias term  : {new_bias:.2f}")

6. Check if the model has converged either by reaching the maximum number of allowed iterations or by seeing that coefficients aren’t changing much anymore. If not converged, return to step 3 and repeat the process.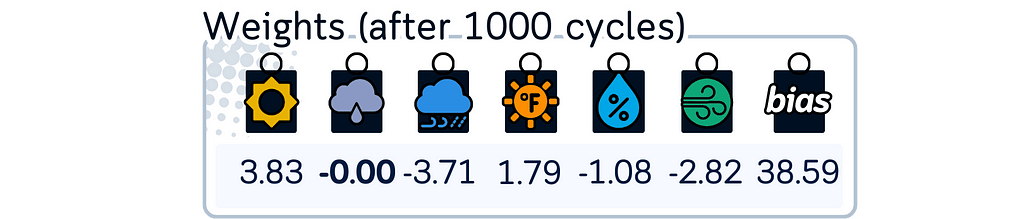

from sklearn.linear_model import ElasticNet

# Fit Lasso from scikit-learn
elasticnet = Lasso(alpha=1) # Default value is 1000 cycle
elasticnet.fit(X_train_scaled, y_train)

# Print results
print("\nCoefficients after 1000 cycles:")
print(f"Bias term  : {elasticnet.intercept_:.2f}")
for feature, coef in zip(X_train_scaled.columns, elasticnet.coef_):
   print(f"{feature:11}: {coef:.2f}")

Test Step

The prediction process remains the same as OLS — multiply new data points by the coefficients:

Lasso Regression

Elastic Net Regression

Evaluation Step

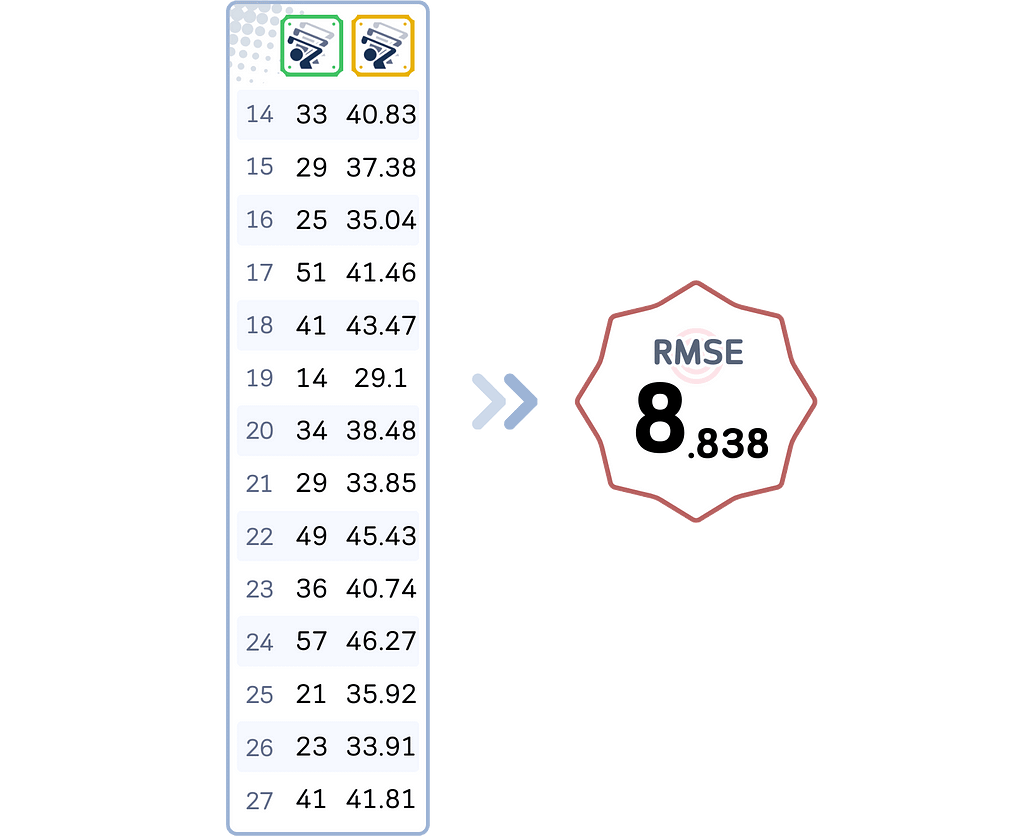
We can do the same process for all data points. For our dataset, here’s the final result with the RMSE as well:

Lasso Regression

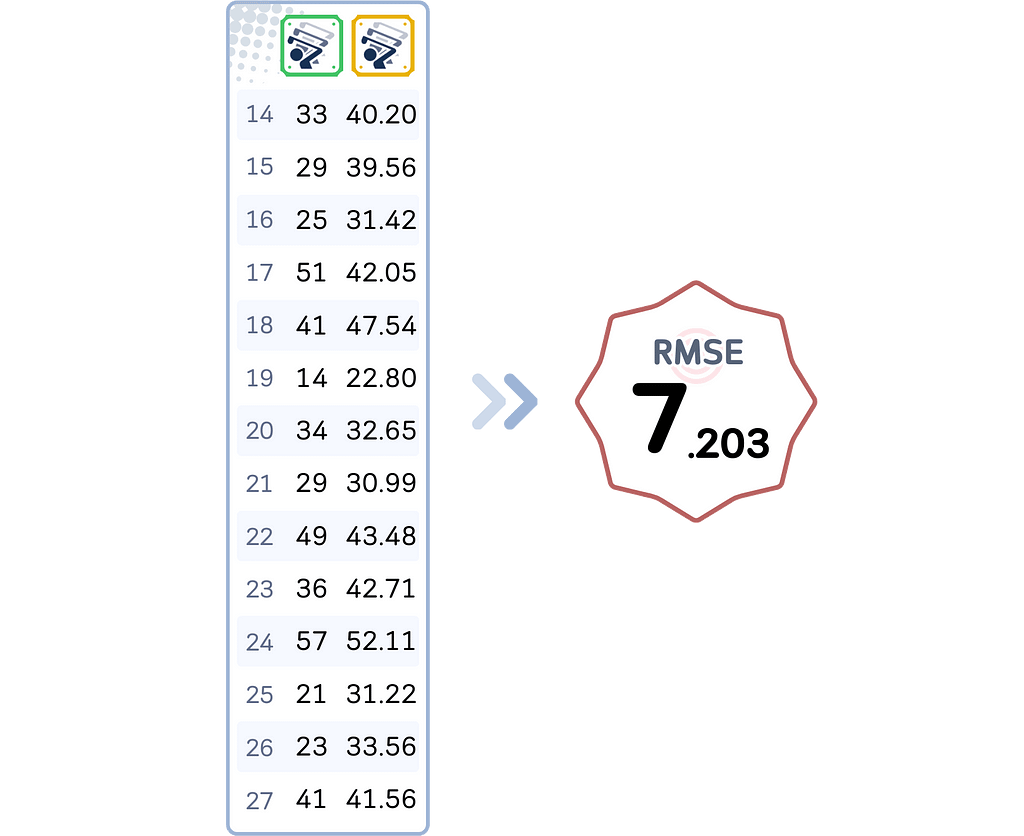
Elastic Net Regression

Key Parameters

Lasso Regression

Lasso regression uses coordinate descent to solve the optimization problem. Here are the key parameters for that:

• alpha (λ): Controls how strongly to penalize large coefficients. Higher values force more coefficients to become exactly zero. Default is 1.0.
• max_iter: Sets the maximum number of cycles the algorithm will update its solution in search of the best result. Default is 1000.
• tol: Sets how small the change in coefficients needs to be before the algorithm decides it has found a good enough solution. Default is 0.0001.

Elastic Net Regression

Elastic Net regression combines two types of penalties and also uses coordinate descent. Here are the key parameters for that:

• alpha (λ): Controls the overall strength of both penalties together. Higher values mean stronger penalties. Default is 1.0.
• l1_ratio (α): Sets how much to use each type of penalty. A value of 0 uses only Ridge penalty, while 1 uses only Lasso penalty. Values between 0 and 1 use both. Default is 0.5.
• max_iter: Maximum number of iterations for the coordinate descent algorithm. Default is 1000 iterations.
• tol: Tolerance for the optimization convergence, similar to Lasso. Default is 1e-4.

Note: Not to be confused, in scikit-learn’s code, the regularization parameter is called alpha, but in mathematical notation it’s typically written as λ (lambda). Similarly, the mixing parameter is called l1_ratio in code but written as α (alpha) in mathematical notation. We use the mathematical symbols here to match standard textbook notation.

Model Comparison: OLS vs Lasso vs Ridge vs Elastic Net

With Elastic Net, we can actually explore different types of linear regression models by adjusting the parameters:

• When alpha = 0, we get Ordinary Least Squares (OLS)
• When alpha > 0 and l1_ratio = 0, we get Ridge regression
• When alpha > 0 and l1_ratio = 1, we get Lasso regression
• When alpha > 0 and 0 < l1_ratio < 1, we get Elastic Net regression

In practice, it is a good idea to explore a range of alpha values (like 0.0001, 0.001, 0.01, 0.1, 1, 10, 100) and l1_ratio values (like 0, 0.25, 0.5, 0.75, 1), preferably using cross-validation to find the best combination.

Here, let’s see how the model coefficients, bias terms, and test RMSE change with different regularization strengths (λ) and mixing parameters (l1_ratio).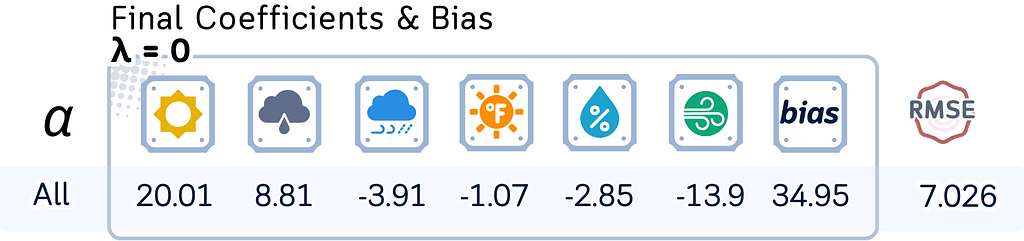

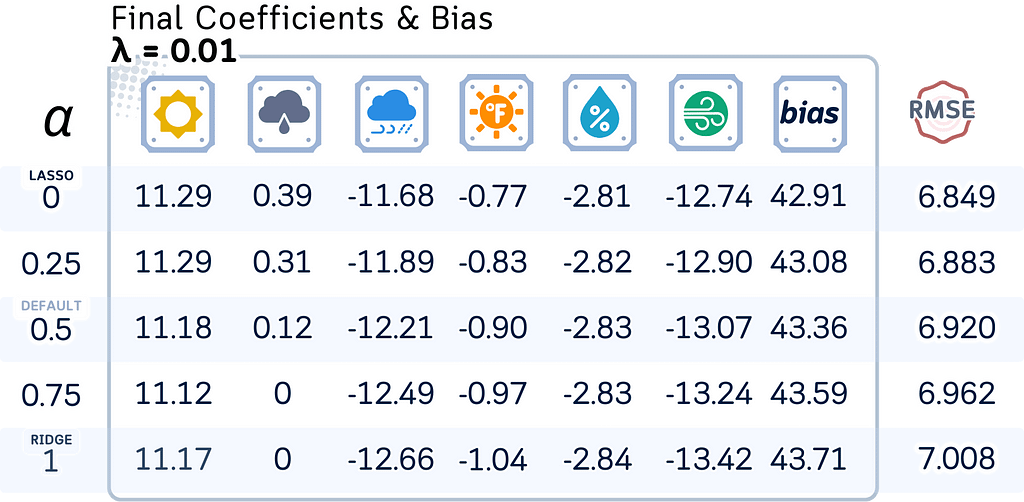
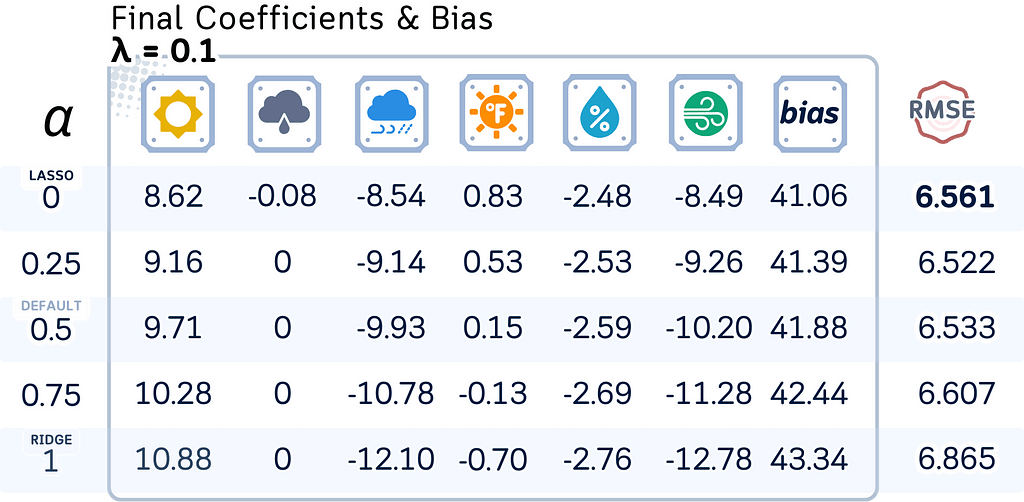
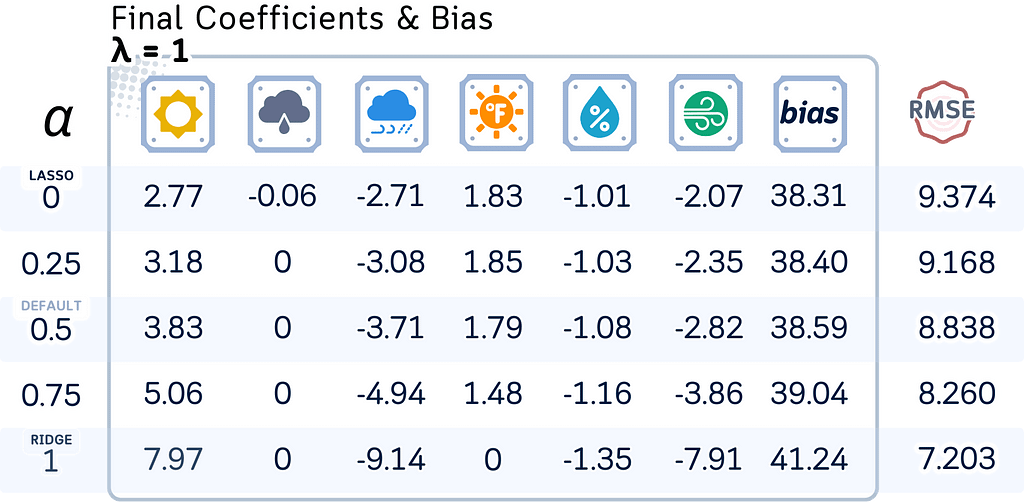
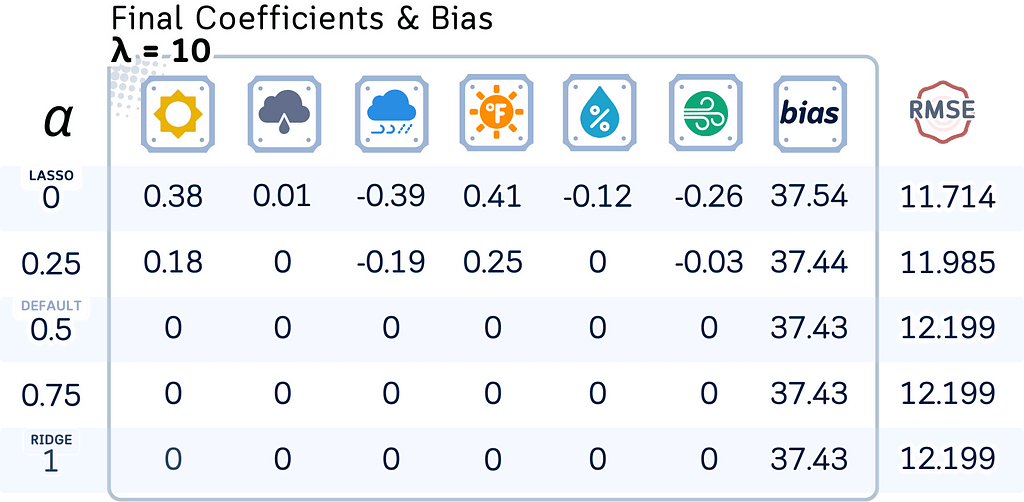
# Define parameters
l1_ratios = [0, 0.25, 0.5, 0.75, 1]
lambdas = [0, 0.01, 0.1, 1, 10]
feature_names = X_train_scaled.columns

# Create a dataframe for each lambda value
for lambda_val in lambdas:
    # Initialize list to store results
    results = []
    rmse_values = []
    
    # Fit ElasticNet for each l1_ratio
    for l1_ratio in l1_ratios:
        # Fit model
        en = ElasticNet(alpha=lambda_val, l1_ratio=l1_ratio)
        en.fit(X_train_scaled, y_train)
        
        # Calculate RMSE
        y_pred = en.predict(X_test_scaled)
        rmse = root_mean_squared_error(y_test, y_pred)
        
        # Store coefficients and RMSE
        results.append(list(en.coef_.round(2)) + [round(en.intercept_,2),round(rmse,3)])
    
    # Create dataframe with RMSE column
    columns = list(feature_names) + ['Bias','RMSE']
    df = pd.DataFrame(results, index=l1_ratios, columns=columns)
    df.index.name = f'λ = {lambda_val}'
    
    print(df)

Note: Even though Elastic Net can do what OLS, Ridge, and Lasso do by changing its parameters, it’s better to use the specific command made for each type of regression. In scikit-learn, use LinearRegression for OLS, Ridge for Ridge regression, and Lasso for Lasso regression. Only use Elastic Net when you want to combine both Lasso and Ridge's special features together.

Final Remarks: Which Regression Method Should You Use?

Let’s break down when to use each method.

Start with Ordinary Least Squares (OLS) when you have more samples than features in your dataset, and when your features don’t strongly predict each other.

Ridge Regression works well when you have the opposite situation — lots of features compared to your number of samples. It’s also great when your features are strongly connected to each other.

Lasso Regression is best when you want to discover which features actually matter for your predictions. It will automatically set unimportant features to zero, making your model simpler.

Elastic Net combines the strengths of both Ridge and Lasso. It’s useful when you have groups of related features and want to either keep or remove them together. If you’ve tried Ridge and Lasso separately and weren’t happy with the results, Elastic Net might give you better predictions.

A good strategy is to start with Ridge if you want to keep all your features. You can move on to Lasso if you want to identify the important ones. If neither gives you good results, then move on to Elastic Net.

???? Lasso and Elastic Net Code Summarized

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.compose import ColumnTransformer
from sklearn.metrics import root_mean_squared_error
from sklearn.linear_model import Lasso  #, ElasticNet

# Create dataset
data = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 
                'rain', 'sunny', 'overcast', 'overcast', 'rain', 'sunny', 'overcast', 'rain', 'sunny', 
                'sunny', 'rain', 'overcast', 'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
    'Temperature': [85, 80, 83, 70, 68, 65, 64, 72, 69, 75, 75, 72, 81, 71, 81, 74, 76, 78, 82, 
                   67, 85, 73, 88, 77, 79, 80, 66, 84],
    'Humidity': [85, 90, 78, 96, 80, 70, 65, 95, 70, 80, 70, 90, 75, 80, 88, 92, 85, 75, 92, 
                 90, 85, 88, 65, 70, 60, 95, 70, 78],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, 
             True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
    'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29, 25, 51, 41, 
                    14, 34, 29, 49, 36, 57, 21, 23, 41]
}

# Process data
df = pd.get_dummies(pd.DataFrame(data), columns=['Outlook'], prefix='', prefix_sep='', dtype=int)
df['Wind'] = df['Wind'].astype(int)
df = df[['sunny','overcast','rain','Temperature','Humidity','Wind','Num_Players']]

# Split data
X, y = df.drop(columns='Num_Players'), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)

# Scale numerical features
numerical_cols = ['Temperature', 'Humidity']
ct = ColumnTransformer([('scaler', StandardScaler(), numerical_cols)], remainder='passthrough')

# Transform data
X_train_scaled = pd.DataFrame(
    ct.fit_transform(X_train),
    columns=numerical_cols + [col for col in X_train.columns if col not in numerical_cols],
    index=X_train.index
)
X_test_scaled = pd.DataFrame(
    ct.transform(X_test),
    columns=X_train_scaled.columns,
    index=X_test.index
)

# Initialize and train the model
model = Lasso(alpha=0.1)  # Option 1: Lasso Regression (alpha is the regularization strength, equivalent to λ, uses coordinate descent)
#model = ElasticNet(alpha=0.1, l1_ratio=0.5)  # Option 2: Elastic Net Regression (alpha is the overall regularization strength, and l1_ratio is the mix between L1 and L2, uses coordinate descent)

# Fit the model
model.fit(X_train_scaled, y_train)

# Make predictions
y_pred = model.predict(X_test_scaled)

# Calculate and print RMSE
rmse = root_mean_squared_error(y_test, y_pred)
print(f"RMSE: {rmse:.4f}")

# Additional information about the model
print("\nModel Coefficients:")
for feature, coef in zip(X_train_scaled.columns, model.coef_):
    print(f"{feature:13}: {coef:.2f}")
print(f"Intercept    : {model.intercept_:.2f}")

Further Reading

For a detailed explanation of Lasso Regression and Elastic Net Regression, and its implementation in scikit-learn, readers can refer to their official documentation. It provides comprehensive information on their usage and parameters.

Technical Environment

This article uses Python 3.7 and scikit-learn 1.5. While the concepts discussed are generally applicable, specific code implementations may vary slightly with different versions

About the Illustrations

Unless otherwise noted, all images are created by the author, incorporating licensed design elements from Canva Pro.

???????????? ???????????????? ???????????????????????????????????????? ???????????????????????????????????????? ????????????????:

Regression Algorithms

???????????? ???????????????????? ???????????????? ????????????????:

• Classification Algorithms
• Ensemble Learning

Lasso and Elastic Net Regressions, Explained: A Visual Guide with Code Examples was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.