Understanding DDPG: The Algorithm That Solves Continuous Action Control Challenges
Discover how DDPG solves the puzzle of continuous action control, unlocking possibilities in AI-driven medical robotics.Imagine you’re controlling a robotic arm in a surgical procedure. Discrete actions might be:Move up,Move down,Grab, orReleaseThese are clear, direct commands, easy to execute in simple scenarios.But what about performing delicate movements, such as:Move the arm by 0.5 mm to avoid damaging the tissue,Apply a force of 3N for tissue compression, orRotate the wrist by 15° to adjust the incision angle?In these situations, you need more than just choosing an action — you must decide how much of that action is needed. This is the world of continuous action spaces, and this is where Deep Deterministic Policy Gradient (DDPG) shines!Traditional methods like Deep Q-Networks (DQN) work well with discrete actions but struggle with continuous ones. Deterministic Policy Gradient (DPG) on the other hand, tackled this issue but faced challenges with poor exploration and instability. DDPG which was first introduced in T P. Lillicrap et al’s paper combines the strengths of DPG and DQN to improve stability and performance in environments with continuous action spaces.In this post, we will discuss the theory and architecture behind DDPG, look at an implementation of it on Python, evaluate its performance (by testing it on MountainCarContinuous game) and briefly discuss how DDPG can be used in the bioengineering field.DDPG ArchitectureUnlike DQN, which evaluates every possible state-action pair to find the best action (impossible in continuous spaces due to infinite combinations), DPG uses an Actor-Critic architecture. The Actor learns a policy that directly maps states to actions, avoiding exhaustive searches and focusing on learning the best action for each state.However, DPG faces two main challenges:It is a deterministic algorithm which limits exploration of the action space.It cannot use neural networks effectively due to instability in the learning process.DDPG improves DPG by introducing exploration noise via the Ornstein-Uhlenbeck process and stabilising training with Batch Normalisation and DQN techniques like Replay Buffer and Target Networks.With these enhancements, DDPG is well-suited to train agents in continuous action spaces, such as controlling robotic systems in bioengineering applications.Now, let’s explore the key components of the DDPG model!Actor-Critic FrameworkActor (Policy Network): Tells the agent which action to take given the state it is in. The network’s parameters (i.e. weights) are represented by θμ.Tip! Think of the Actor Network as the decision-maker: it maps the current state to a single action.Critic (Q-value Network): Evaluates how good the action taken by the actor by estimating the Q-value of that state-action pair.Tip! Think of the Critic Network as the evaluator, it assigns a quality score to each action and helps improve the Actor’s policy to make sure it indeed generates the best action to take in each given state.Note! The critic will use the estimated Q-value for two things:To improve the Actor’s policy (Actor Policy Update).The Actor’s goal is to adjust its parameters (θμ) so that it outputs actions that maximise the critic’s Q-value.To do so, the Actor needs to understand both how the selected action a affects the Critic’s Q-value and how its internal parameters affect its Policy which is done through this Policy Gradient equation (it is the mean of all the gradients calculated from the mini-batch):2. To improve its own network (Critic Q-value Network Update) by minimising the loss function below.Where N is the number of experiences sampled in the mini-batch and y_i is the target Q-value calculated as follows.Replay BufferAs the agent explores the environment, past experiences (state, action, reward, next state) are stored as tuples (s, a, r, s′) in the replay buffer. During training, mini-batches consisting of some of these experiences are then randomly sampled to train the agent.Question! How does replay buffer actually reduce instability?By randomly sampling experiences, the replay buffer breaks the correlation between consecutive samples, reducing bias and leading to more stable training.Target NetworksTarget Networks are slowly updated copies of the Actor and Critic. They provide stable Q-value targets, preventing rapid changes and ensuring smooth, consistent updates.Question! How do target networks actually reduce instability?Without the Critic target network, the target Q-value is calculated directly from the Critic Q-value network, which is updated continuously. This causes the target Q-value to shift at each step, creating a “moving target” problem. As a result, the Critic ends up chasing a constantly changing target, making training unstable.Additionally, since the Actor relies on the Critic’s feedback, errors in one network can amplify errors in the other, creating an interdependent loop of instability.By introducing target networks that are updated gradua

Discover how DDPG solves the puzzle of continuous action control, unlocking possibilities in AI-driven medical robotics.
Imagine you’re controlling a robotic arm in a surgical procedure. Discrete actions might be:
- Move up,
- Move down,
- Grab, or
- Release
These are clear, direct commands, easy to execute in simple scenarios.
But what about performing delicate movements, such as:
- Move the arm by 0.5 mm to avoid damaging the tissue,
- Apply a force of 3N for tissue compression, or
- Rotate the wrist by 15° to adjust the incision angle?
In these situations, you need more than just choosing an action — you must decide how much of that action is needed. This is the world of continuous action spaces, and this is where Deep Deterministic Policy Gradient (DDPG) shines!
Traditional methods like Deep Q-Networks (DQN) work well with discrete actions but struggle with continuous ones. Deterministic Policy Gradient (DPG) on the other hand, tackled this issue but faced challenges with poor exploration and instability. DDPG which was first introduced in T P. Lillicrap et al’s paper combines the strengths of DPG and DQN to improve stability and performance in environments with continuous action spaces.
In this post, we will discuss the theory and architecture behind DDPG, look at an implementation of it on Python, evaluate its performance (by testing it on MountainCarContinuous game) and briefly discuss how DDPG can be used in the bioengineering field.
DDPG Architecture
Unlike DQN, which evaluates every possible state-action pair to find the best action (impossible in continuous spaces due to infinite combinations), DPG uses an Actor-Critic architecture. The Actor learns a policy that directly maps states to actions, avoiding exhaustive searches and focusing on learning the best action for each state.
However, DPG faces two main challenges:
- It is a deterministic algorithm which limits exploration of the action space.
- It cannot use neural networks effectively due to instability in the learning process.
DDPG improves DPG by introducing exploration noise via the Ornstein-Uhlenbeck process and stabilising training with Batch Normalisation and DQN techniques like Replay Buffer and Target Networks.
With these enhancements, DDPG is well-suited to train agents in continuous action spaces, such as controlling robotic systems in bioengineering applications.
Now, let’s explore the key components of the DDPG model!
Actor-Critic Framework
- Actor (Policy Network): Tells the agent which action to take given the state it is in. The network’s parameters (i.e. weights) are represented by θμ.
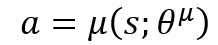
Tip! Think of the Actor Network as the decision-maker: it maps the current state to a single action.
- Critic (Q-value Network): Evaluates how good the action taken by the actor by estimating the Q-value of that state-action pair.
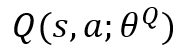
Tip! Think of the Critic Network as the evaluator, it assigns a quality score to each action and helps improve the Actor’s policy to make sure it indeed generates the best action to take in each given state.
Note! The critic will use the estimated Q-value for two things:
- To improve the Actor’s policy (Actor Policy Update).
The Actor’s goal is to adjust its parameters (θμ) so that it outputs actions that maximise the critic’s Q-value.
To do so, the Actor needs to understand both how the selected action a affects the Critic’s Q-value and how its internal parameters affect its Policy which is done through this Policy Gradient equation (it is the mean of all the gradients calculated from the mini-batch):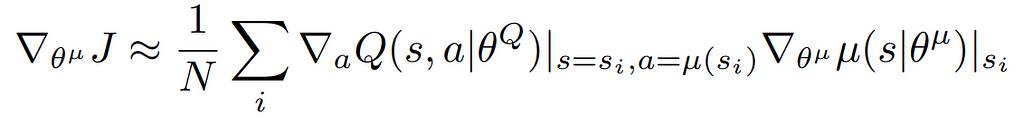
2. To improve its own network (Critic Q-value Network Update) by minimising the loss function below.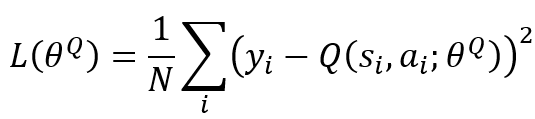
Where N is the number of experiences sampled in the mini-batch and y_i is the target Q-value calculated as follows.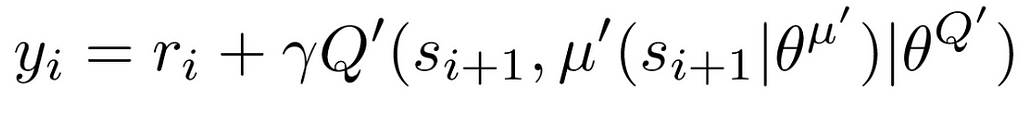
Replay Buffer
As the agent explores the environment, past experiences (state, action, reward, next state) are stored as tuples (s, a, r, s′) in the replay buffer. During training, mini-batches consisting of some of these experiences are then randomly sampled to train the agent.
Question! How does replay buffer actually reduce instability?
By randomly sampling experiences, the replay buffer breaks the correlation between consecutive samples, reducing bias and leading to more stable training.
Target Networks
Target Networks are slowly updated copies of the Actor and Critic. They provide stable Q-value targets, preventing rapid changes and ensuring smooth, consistent updates.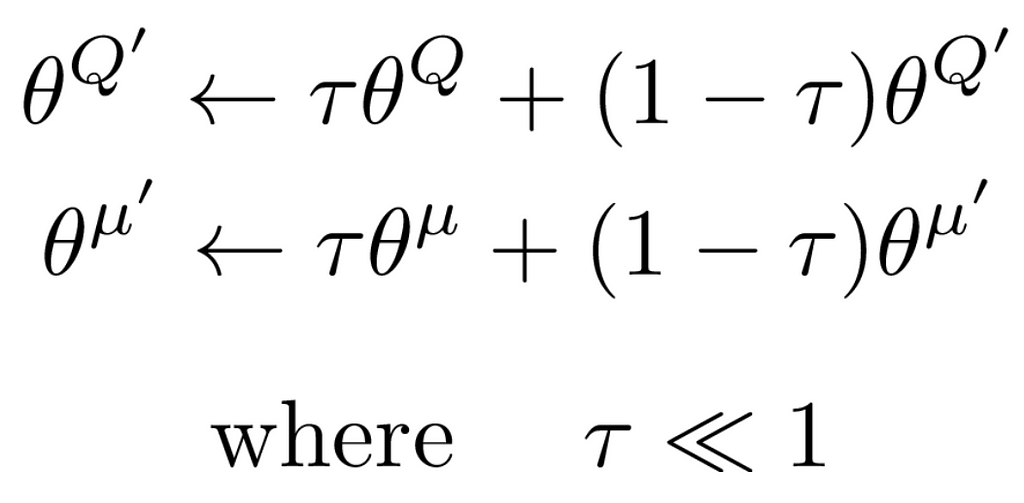
Question! How do target networks actually reduce instability?
Without the Critic target network, the target Q-value is calculated directly from the Critic Q-value network, which is updated continuously. This causes the target Q-value to shift at each step, creating a “moving target” problem. As a result, the Critic ends up chasing a constantly changing target, making training unstable.
Additionally, since the Actor relies on the Critic’s feedback, errors in one network can amplify errors in the other, creating an interdependent loop of instability.
By introducing target networks that are updated gradually with a soft update rule, we ensure the target Q-value remains more consistent, reducing abrupt changes and improving learning stability.
Batch Normalisation
Batch Normalisation standardises the inputs to each layer of the neural network, ensuring mean of zero and a unit variance.
Question! How does batch normalisation actually reduce instability?
Samples drawn from the replay buffer may have different distributions than real-time data, leading to instability during network updates.
Batch normalisation ensures consistent scaling of inputs to prevent erratic updates caused by varying input distributions.
Exploration Noise
Since the Actor’s policy is deterministic, exploration noise is added to actions during training to encourage the agent to explore the as much of the action space as possible.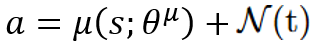
On the DDPG publication, the authors used the Ornstein-Uhlenbeck process to generate temporally correlated noise, in order to mimick real-world system dynamics.
DDPG Pseudocode: A Step-by-Step Breakdown

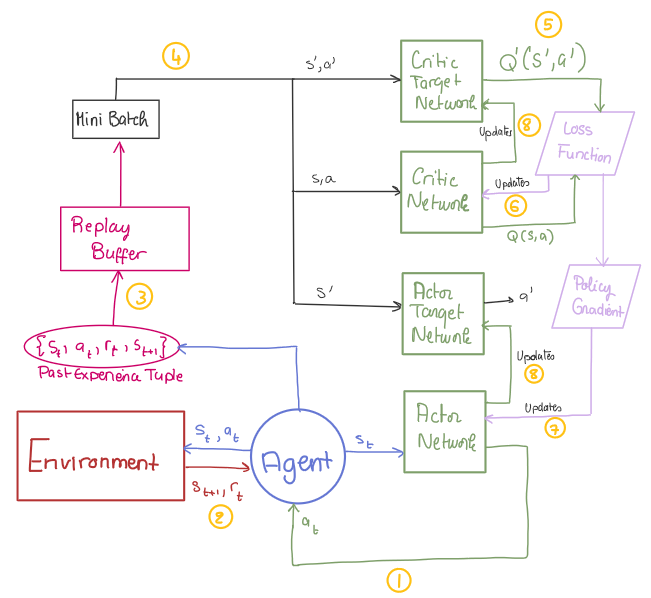
- Define Actor and Critic Networks
class Actor(nn.Module):
"""
Actor network for the DDPG algorithm.
"""
def __init__(self, state_dim, action_dim, max_action,use_batch_norm):
"""
Initialise the Actor's Policy network.
:param state_dim: Dimension of the state space
:param action_dim: Dimension of the action space
:param max_action: Maximum value of the action
"""
super(Actor, self).__init__()
self.bn1 = nn.LayerNorm(HIDDEN_LAYERS_ACTOR) if use_batch_norm else nn.Identity()
self.bn2 = nn.LayerNorm(HIDDEN_LAYERS_ACTOR) if use_batch_norm else nn.Identity()
self.l1 = nn.Linear(state_dim, HIDDEN_LAYERS_ACTOR)
self.l2 = nn.Linear(HIDDEN_LAYERS_ACTOR, HIDDEN_LAYERS_ACTOR)
self.l3 = nn.Linear(HIDDEN_LAYERS_ACTOR, action_dim)
self.max_action = max_action
def forward(self, state):
"""
Forward propagation through the network.
:param state: Input state
:return: Action
"""
a = torch.relu(self.bn1(self.l1(state)))
a = torch.relu(self.bn2(self.l2(a)))
return self.max_action * torch.tanh(self.l3(a))
class Critic(nn.Module):
"""
Critic network for the DDPG algorithm.
"""
def __init__(self, state_dim, action_dim,use_batch_norm):
"""
Initialise the Critic's Value network.
:param state_dim: Dimension of the state space
:param action_dim: Dimension of the action space
"""
super(Critic, self).__init__()
self.bn1 = nn.BatchNorm1d(HIDDEN_LAYERS_CRITIC) if use_batch_norm else nn.Identity()
self.bn2 = nn.BatchNorm1d(HIDDEN_LAYERS_CRITIC) if use_batch_norm else nn.Identity()
self.l1 = nn.Linear(state_dim + action_dim, HIDDEN_LAYERS_CRITIC)
self.l2 = nn.Linear(HIDDEN_LAYERS_CRITIC, HIDDEN_LAYERS_CRITIC)
self.l3 = nn.Linear(HIDDEN_LAYERS_CRITIC, 1)
def forward(self, state, action):
"""
Forward propagation through the network.
:param state: Input state
:param action: Input action
:return: Q-value of state-action pair
"""
q = torch.relu(self.bn1(self.l1(torch.cat([state, action], 1))))
q = torch.relu(self.bn2(self.l2(q)))
return self.l3(q)
- Define Replay Buffer
A ReplayBuffer class is implemented to store and sample the transition tuples (s, a, r, s’) discussed in the previous section to enable mini-batch off-policy learning.
class ReplayBuffer:
def __init__(self, capacity):
self.buffer = deque(maxlen=capacity)
def push(self, state, action, reward, next_state, done):
self.buffer.append((state, action, reward, next_state, done))
def sample(self, batch_size):
return random.sample(self.buffer, batch_size)
def __len__(self):
return len(self.buffer)
- Define OU Noise class
An OUNoise class is added to generate exploration noise, helping the agent explore the action space more effectively.
"""
Taken from https://github.com/vitchyr/rlkit/blob/master/rlkit/exploration_strategies/ou_strategy.py
"""
class OUNoise(object):
def __init__(self, action_space, mu=0.0, theta=0.15, max_sigma=0.3, min_sigma=0.3, decay_period=100000):
self.mu = mu
self.theta = theta
self.sigma = max_sigma
self.max_sigma = max_sigma
self.min_sigma = min_sigma
self.decay_period = decay_period
self.action_dim = action_space.shape[0]
self.low = action_space.low
self.high = action_space.high
self.reset()
def reset(self):
self.state = np.ones(self.action_dim) * self.mu
def evolve_state(self):
x = self.state
dx = self.theta * (self.mu - x) + self.sigma * np.random.randn(self.action_dim)
self.state = x + dx
return self.state
def get_action(self, action, t=0):
ou_state = self.evolve_state()
self.sigma = self.max_sigma - (self.max_sigma - self.min_sigma) * min(1.0, t / self.decay_period)
return np.clip(action + ou_state, self.low, self.high)
- Define the DDPG agent
A DDPG class was defined and it encapsulates the agent’s behavior:
- Initialisation: Creates Actor and Critic networks, along with their target counterparts and the replay buffer.
class DDPG():
"""
Deep Deterministic Policy Gradient (DDPG) agent.
"""
def __init__(self, state_dim, action_dim, max_action,use_batch_norm):
"""
Initialise the DDPG agent.
:param state_dim: Dimension of the state space
:param action_dim: Dimension of the action space
:param max_action: Maximum value of the action
"""
# [STEP 0]
# Initialise Actor's Policy network
self.actor = Actor(state_dim, action_dim, max_action,use_batch_norm)
# Initialise Actor target network with same weights as Actor's Policy network
self.actor_target = Actor(state_dim, action_dim, max_action,use_batch_norm)
self.actor_target.load_state_dict(self.actor.state_dict())
self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=ACTOR_LR)
# Initialise Critic's Value network
self.critic = Critic(state_dim, action_dim,use_batch_norm)
# Initialise Crtic's target network with same weights as Critic's Value network
self.critic_target = Critic(state_dim, action_dim,use_batch_norm)
self.critic_target.load_state_dict(self.critic.state_dict())
self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=CRITIC_LR)
# Initialise the Replay Buffer
self.replay_buffer = ReplayBuffer(BUFFER_SIZE)
2. Action Selection: The select_action method chooses actions based on the current policy.
def select_action(self, state):
"""
Select an action given the current state.
:param state: Current state
:return: Selected action
"""
state = torch.FloatTensor(state.reshape(1, -1))
action = self.actor(state).cpu().data.numpy().flatten()
return action
- 3. Training: The train method defines how the networks are updated using experiences from the replay buffer.
Note! Since the paper introduced the use of target networks and batch normalisation to improve stability, I designed the train method to allow us to toggle these methods on or off. This lets us compare the agent’s performance with and without them. See code below for exact implementation.
def train(self, use_target_network,use_batch_norm):
"""
Train the DDPG agent.
:param use_target_network: Whether to use target networks or not
:param use_batch_norm: Whether to use batch normalisation or not
"""
if len(self.replay_buffer) < BATCH_SIZE:
return
# [STEP 4]. Sample a batch from the replay buffer
batch = self.replay_buffer.sample(BATCH_SIZE)
state, action, reward, next_state, done = map(np.stack, zip(*batch))
state = torch.FloatTensor(state)
action = torch.FloatTensor(action)
next_state = torch.FloatTensor(next_state)
reward = torch.FloatTensor(reward.reshape(-1, 1))
done = torch.FloatTensor(done.reshape(-1, 1))
# Critic Network update #
if use_target_network:
target_Q = self.critic_target(next_state, self.actor_target(next_state))
else:
target_Q = self.critic(next_state, self.actor(next_state))
# [STEP 5]. Calculate target Q-value (y_i)
target_Q = reward + (1 - done) * GAMMA * target_Q
current_Q = self.critic(state, action)
critic_loss = nn.MSELoss()(current_Q, target_Q.detach())
# [STEP 6]. Use gradient descent to update weights of the Critic network
# to minimise loss function
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
# Actor Network update #
actor_loss = -self.critic(state, self.actor(state)).mean()
# [STEP 7]. Use gradient descent to update weights of the Actor network
# to minimise loss function and maximise the Q-value => choose the action that yields the highest cumulative reward
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
# [STEP 8]. Update target networks
if use_target_network:
for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()):
target_param.data.copy_(TAU * param.data + (1 - TAU) * target_param.data)
for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
target_param.data.copy_(TAU * param.data + (1 - TAU) * target_param.data)
- Train the DDPG agent
Bringing all the defined classes and methods together, we can train the DDPG agent. My train_dppg function follows the pseudocode and DDPG model diagram structure.
Tip: To make it easier for you to understand, I’ve labeled each code section with the corresponding step number from both the pseudocode and diagram. Hope that helps! :)
def train_ddpg(use_target_network, use_batch_norm, num_episodes=NUM_EPISODES):
"""
Train the DDPG agent.
:param use_target_network: Whether to use target networks
:param use_batch_norm: Whether to use batch normalization
:param num_episodes: Number of episodes to train
:return: List of episode rewards
"""
agent = DDPG(state_dim, action_dim, 1,use_batch_norm)
episode_rewards = []
noise = OUNoise(env.action_space)
for episode in range(num_episodes):
state= env.reset()
noise.reset()
episode_reward = 0
done = False
step=0
while not done:
action_actor = agent.select_action(state)
action = noise.get_action(action_actor,step) # Add noise for exploration
next_state, reward, done,_= env.step(action)
done = float(done) if isinstance(done, (bool, int)) else float(done[0])
agent.replay_buffer.push(state, action, reward, next_state, done)
if len(agent.replay_buffer) > BATCH_SIZE:
agent.train(use_target_network,use_batch_norm)
state = next_state
episode_reward += reward
step+=1
episode_rewards.append(episode_reward)
if (episode + 1) % 10 == 0:
print(f"Episode {episode + 1}: Reward = {episode_reward}")
return agent, episode_rewards
Performance and Results: Evaluating DDPG’s Effectiveness
DDPG’s effectiveness in a continuous action space was tested in the MountainCarContinuous-v0 environment, where the agent learns to where the agent learns to gain momentum to drive the car up a steep hill. The results show that using Target Networks and Batch Normalisation leads to faster convergence, higher rewards, and more stable learning than other configurations.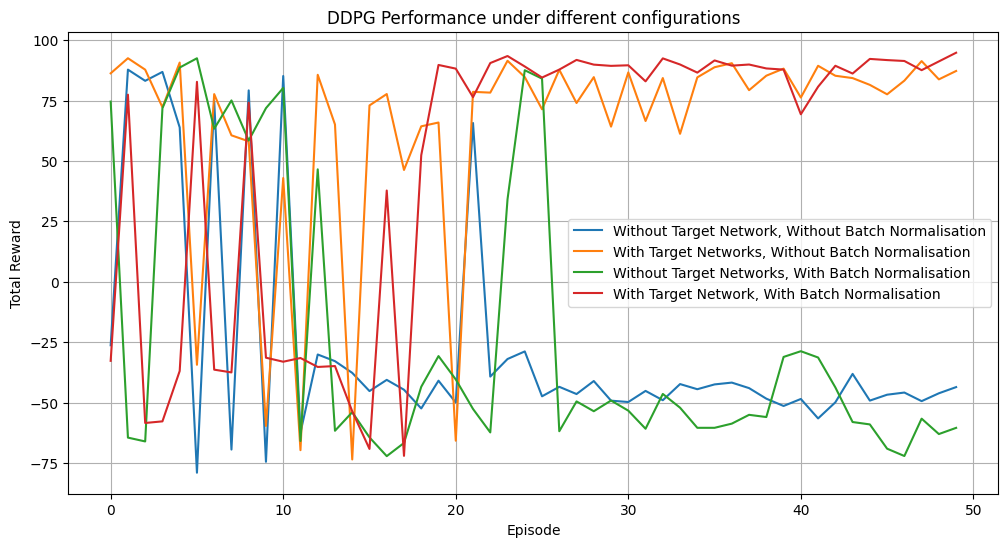
Note! You can implement this yourself on any environment of your choice by running the code which can be found on my GitHub as is and simply changing the environment’s name as needed!
DDPG in Bioengineering: Unlocking Precision and Adaptability
Through this blog post, we’ve seen that DDPG is a powerful algorithm for training agents in environments with continuous action spaces. By combining techniques from both DPG and DQN, DDPG improves exploration, stability, and performance — key factors for applications in robotic surgery and bioengineering.
Imagine a robotic surgeon, like the da Vinci system, using DDPG to control fine movements in real-time, ensuring precise adjustments without any errors. With DDPG, the robot could adjust its arm’s position by millimeters, apply exact force when suturing, or even make slight wrist rotations for an optimal incision. Such real-time precision could transform surgical outcomes, reduce recovery time, and minimise human error.
But DDPG’s potential goes beyond surgery. It’s already advancing bioengineering, enabling robotic prosthetics and assistive devices to replicate the natural motion of human limbs (check out this super interesting article!).
Now that we’ve covered the theory behind DDPG, it’s time for you to explore its implementation. Start with simple examples and gradually dive into more complex scenarios!
References
- Lillicrap TP, Hunt JJ, Pritzel A, Heess N, Erez T, Tassa Y, et al. Continuous control with deep reinforcement learning [Internet]. arXiv; 2019. Available from: http://arxiv.org/abs/1509.02971
Understanding DDPG: The Algorithm That Solves Continuous Action Control Challenges was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.













